Сегодня я расскажу, как я применил алгоритмы глубинного обучения с подкреплением для управления роботом. Вкратце, поведаю о том, как создать «чёрный ящик с нейросетями», который на входе принимает архитектуру робота, а на выходе выдаёт алгоритм, способный им управлять.

Основой решения является алгоритм Advantage Actor Critic (A2C) с оценкой Advantage через Generalized Advantage Estimation (GAE).

Под катом математика, реализация на TensorFlow и множество демок того, к каким способам ходьбы сошлись алгоритмы.

Содержание:

— Заключение

В этой статье будем учить робота ходить в симуляции MuJoCo. Пропустим описание шага с созданием модели робота и Python интерфейса к среде, т.к. там ничего интересного нет. Чтобы разобраться, достаточно посмотреть на демки в самой MuJoCo и исходники MuJoCo-сред в Gym OpenAI.

На входе у агента будет множество чисел из MuJoCo: относительные позиции, углы вращения, скорости, ускорения частей тела робота, и т.д. В сумме порядка ~800 фичей. Используем Deep Learning подход и не будем разбираться, что они на самом деле означают. Главное, что в этом наборе чисел будет достаточно информации, чтобы агент мог понять, что с ним происходит.

На выходе будем ожидать 18 чисел — количество степеней свободы робота, которые означают углы поворота шарниров, на которых закреплены конечности.

И наконец, целью агента будет максимизировать суммарную награду (reward) за эпизод. Будем завершать эпизод, если робот упал или если прошло 3000 шагов (15 секунд). Каждый шаг будем награждать агента по следующей формуле:

Т.е. целью агента будет увеличивать свою координату $$ и не падать до конца эпизода.

Итак, задача поставлена: найти функцию $$, для которой награда за эпизод будет наибольшей. Звучит не очень, правда? :) Посмотрим, как с такой задачей справится Deep Reinforcement Learning.

Современные подходы к решению задачи движения ходячих роботов состоят из классических практик робототехники из разделов optimal control и trajectory optimization: LQR, QP, выпуклая оптимизация. Подробнее: публикация коллектива Boston Dynamics о роботе Atlas.

Эти техники являются своего рода «хардкодингом», поскольку требуют внесения многих деталей задачи напрямую в управляющий алгоритм. В них нет обучающихся систем — оптимизация происходит «на месте».

С другой стороны, Reinforcement Learning (далее RL) не требует внесения гипотез в алгоритм, делая решение задачи более общим и масштабируемым.

Постановка задачи Reinforcement Learning

Источник

В задаче RL мы рассматриваем взаимодействие агента и среды как последовательность пар (state, reward) и переходы между ними — action.

Определим терминологию:

• $$ — policy, стратегия поведения агента, условная вероятность,
• $$ — action рассматриваем как случайную величину из распределения $$,
  Мы могли бы рассматривать policy как функцию $$, но мы хотим сделать действия агента стохастическими, что способствует exploration. Т.е. мы с некоторой вероятностью делаем не совсем те действия, которые выбирает агент.
• $$ — траектория, пройденная агентом, последовательность $$.

Задача агента — максимизировать expected return:

Теперь мы можем сформулировать задачу RL, найти:

где $$ — это оптимальная policy.

Подробнее в материале от OpenAI: OpenAI Spinning Up.

Именно в этом и заключается идея всех методов policy gradient. Строгий вывод этого градиента является несколько хардкорным. Не будем писать его здесь, а оставим ссылку на замечательный материал от OpenAI. Градиент выглядит вот так:

Таким образом loss нашей модели будет таким:

Напомним, что $$, а $$ — это выход нашей модели в тот момент, когда она была в $$. Минус появился за счёт того, что мы хотим максимизировать $$. При обучении мы будем считать градиент на батчах и складывать их с целью уменьшить variance(шум данных за счёт стохастичности среды).

Это уже рабочий алгоритм, называющийся REINFORCE. И он умеет находить решения для некоторых простых сред. Например, «CartPole-v1».

Рассмотрим код агента:

class ActorNetworkDiscrete:
    def __init__(self):
        self.state_ph = tf.placeholder(tf.float32, shape=[None, observation_space])
        l1 = tf.layers.dense(self.state_ph, units=20, activation=tf.nn.relu)
        output_linear = tf.layers.dense(l1, units=action_space)

        output = tf.nn.softmax(output_linear)
        self.action_op = tf.squeeze(tf.multinomial(logits=output_linear,num_samples=1), 
                                    axis=1)

        # Training
        output_log = tf.nn.log_softmax(output_linear)

        self.weight_ph = tf.placeholder(shape=[None], dtype=tf.float32)
        self.action_ph = tf.placeholder(shape=[None], dtype=tf.int32)

        action_one_hot = tf.one_hot(self.action_ph, action_space)
        responsible_output_log = tf.reduce_sum(output_log * action_one_hot, axis=1)
        self.loss = -tf.reduce_mean(responsible_output_log * self.weight_ph)

        optimizer = tf.train.AdamOptimizer(learning_rate=actor_learning_rate)
        self.update_op = optimizer.minimize(self.loss)

actor = ActorNetworkDiscrete()

У нас есть небольшой перцептрон такой архитектуры: (observation_space, 10, action_space)[для CartPole это (4, 10, 2)]. tf.multinomial позволяет выбрать действие взвешенно случайно. Для получения действия нужно вызвать:

action = sess.run(actor.action_op, 
                  feed_dict={actor.state_ph: observation})

И вот так будем его обучать:

batch_generator = generate_batch(environments,
                                 batch_size=batch_size)

for epoch in tqdm_notebook(range(epochs_number)):
    batch = next(batch_generator)

    # Remainder: batch item consists of [state, action, total reward]
    # Train actor
    _, actor_loss = sess.run([actor.update_op, actor.loss], 
                             feed_dict={actor.state_ph: batch[:, 0],
                                        actor.action_ph: batch[:, 1],
                                        actor.weight_ph: batch[:, 2]})

Генератор батчей запускает агента в среде и копит данные для обучения. Элементами батча являются туплы такого вида: $$.

Написать хороший генератор — отдельная задача, где основная сложность — относительная дороговизна вызова sess.run() по сравнению с одним шагом симуляции (даже MuJoCo). Для ускорения работы можно эксплуатировать тот факт, что нейронные сети запускаются на батчах, и использовать много параллельных сред. Даже последовательный запуск их в одном потоке даст значительное ускорение по сравнению с одной средой.

# Vectorized environments with gym-like interface
from baselines.common.vec_env.subproc_vec_env import SubprocVecEnv
from baselines.common.vec_env.dummy_vec_env import DummyVecEnv

def make_env(env_id, seed):
    def _f():
        env = gym.make(env_name)
        env.reset()

        # Desync environments
        for i in range(int(200 * seed // environments_count)):
            env.step(env.action_space.sample())
        return env
    return _f

envs = [make_env(env_name, seed) for seed in range(environments_count)]

# Can be switched to SubprocVecEnv to parallelize on cores 
# (for computationally heavy envs)
envs = DummyVecEnv(envs)


# Source: 
# https://github.com/openai/spinningup/blob/master/spinup/algos/ppo/core.py
def discount_cumsum(x, coef):
    """
    magic from rllab for computing discounted cumulative sums of vectors.
    input: 
        vector x, 
        [x0, 
         x1, 
         x2]
    output:
        [x0 + discount * x1 + discount^2 * x2,  
         x1 + discount * x2,
         x2]
    """
    return scipy.signal.lfilter([1], [1, float(-coef)], x[::-1], axis=0)[::-1]


def generate_batch(envs, batch_size, replay_buffer_size):
    envs_number = envs.num_envs
    observations = [[0 for i in range(observation_space)] for i in range(envs_number)]
    
    # [state, action, discounted reward-to-go]
    replay_buffer = np.empty((0,3), np.float32)
    
    # [state, action, reward] rollout lists for every environment instance
    rollouts = [np.empty((0, 3)) for i in range(envs_number)]

    while True:
        history = {'reward': [], 'max_action': []}
        replay_buffer = replay_buffer[batch_size:]
        
        # Main sampling cycle
        while len(replay_buffer) < replay_buffer_size:
            # Here policy acts in environments. Note that it chooses actions for all
            # environments in one batch, therefore expensive sess.run is called once.
            actions = sess.run(actor.action_op, 
                               feed_dict={actor.state_ph: observations})
            observations_old = observations
            observations, rewards, dones, _ = envs.step(actions)
            
            history['max_action'].append(np.abs(actions).max())
            
            time_point = np.array(list(zip(observations_old, actions, rewards)))
            for i in range(envs_number):
                # Regular python-like append
                rollouts[i] = np.append(rollouts[i], [time_point[i]], axis=0) 
            
            # Process done==True environments
            if dones.all():
                print('WARNING: envs are in sync!! This makes sampling inefficient!')

            done_indexes = np.arange(envs_number)[dones]
            for i in done_indexes:
                rewards_trajectory = rollouts[i][:, 2].copy()
                history['reward'].append(rewards_trajectory.sum())

                rollouts[i][:, 2] = discount_cumsum(rewards_trajectory,
                                                    coef=discount_factor)
                replay_buffer = np.append(replay_buffer, rollouts[i], axis=0)
                rollouts[i] = np.empty((0, 3))
        
        # Shuffle before yield to become closer to i.i.d.
        np.random.shuffle(replay_buffer)
        
        # Truncate replay_buffer to get the most relevant feedback from environment
        replay_buffer = replay_buffer[:replay_buffer_size]
        yield replay_buffer[:batch_size], history

# Make a test yield
a = generate_batch(envs, 8, 64)
# Makes them of equal lenght
for i in range(10):
    next(a)
next(a)[0]

Полученный агент умеет играть в средах с конечным пространством действий. Такой формат не подходит для нашей задачи. Агент, управляющий роботом, должен выдавать вектор из $$, где $$ — количество степеней свобод. (либо можно разбить пространство действий на промежутки и получить задачу с дискретным выходом)

Подробнее о стохастических policy.

Код агента:

epsilon = 1e-8

def gaussian_loglikelihood(x, mu, log_std):
    pre_sum = -0.5 * (((x - mu) / (tf.exp(log_std) + epsilon))**2 + 2 * log_std + np.log(2 * np.pi))
    return tf.reduce_sum(pre_sum, axis=1)

class ActorNetworkContinuous:
    def __init__(self):
        self.state_ph = tf.placeholder(tf.float32, shape=[None, observation_space])

        l1 = tf.layers.dense(self.state_ph, units=100, activation=tf.nn.tanh)
        l2 = tf.layers.dense(l1, units=50, activation=tf.nn.tanh)
        l3 = tf.layers.dense(l2, units=25, activation=tf.nn.tanh)
        mu = tf.layers.dense(l3, units=action_space)

        log_std = tf.get_variable(name='log_std', 
                                  initializer=-0.5 * np.ones(action_space, 
        std = tf.exp(log_std)

        self.action_op = mu + tf.random.normal(shape=tf.shape(mu)) * std

        # Training
        self.weight_ph = tf.placeholder(shape=[None], dtype=tf.float32)
        self.action_ph = tf.placeholder(shape=[None, action_space], dtype=tf.float32)

        action_logprob = gaussian_loglikelihood(self.action_ph, mu, log_std)
        self.loss = -tf.reduce_mean(action_logprob * self.weight_ph)
        
        optimizer = tf.train.AdamOptimizer(learning_rate=actor_learning_rate)
        self.update_op = optimizer.minimize(self.loss)

Часть с обучением ничем не отличается.

Теперь мы, наконец, можем посмотреть, как REINFORCE справится с нашей задачей. Здесь и далее цель агента — продвигаться вправо.

Медленно, но верно ползёт к своей цели.

Reward-to-go

Заметим, что в нашем градиенте есть лишние члены. А именно для каждого шага $$ при взвешивании градиента логарифма мы используем суммарную награду за всю траекторию. Таким образом, оценивая действия агента его достижениями из прошлого. Звучит неправильно, не так ли? Поэтому вот это

$$

станет вот этим

$$

Найдите 10 отличий :)

В то время как присутствие этих членов ничего не портит математически, это сильно зашумляет нам данные. Теперь при обучении агент будет обращать внимание только на те награды, которые получил после конкретного действия.

Вследствие этого улучшения средний reward вырос. Один из полученных агентов научился использовать передние конечности для достижения своей цели:

Уменьшаем variance путём добавления критика

Сутью дальнейших улучшений является уменьшение шума (variance), появляющегося из-за стохастичности переходов между состояниями среды.

В этом нам поможет добавление модели, которая будет предсказывать среднюю сумму наград, полученных агентом, начиная с состояния $$ до конца траектории, т.е. Value-функцию.

$$

$$

$$

Value-функция показывает expected return, если наша policy начнёт игру из конкретного состояния. То же самое с Q-функцией, только ещё фиксируем самое первое действие.

Добавляем критика

Так выглядит градиент при использовании reward-to-go:

$$

Теперь коэффициентом при градиенте логарифма является ни что иное, как сэмпл Value-функции.

$$

Мы взвешиваем градиент логарифма одним сэмплом из какой-то конкретной траектории, что не есть хорошо. Мы можем аппроксимировать Value-функцию какой-нибудь моделью, например нейронной сетью, и спрашивать необходимое значение у неё, тем самым ещё уменьшив variance. Назовём эту модель критиком (Critic) и будем учить её параллельно с policy. Таким образом, формулу градиента можно записать как:

$$

Мы уменьшили variance, но в то же время мы внесли bias в наш алгоритм, так как нейронные сети могут допускать ошибки при аппроксимации. Но компромисс в данной ситуации оказывается хорошим. Такие ситуации в машинном обучении называют bias-variance tradeoff.

Критик будет учить Value-функцию регрессией по сэмплам reward-to-go, собранным в среде. В качестве функции ошибки возьмём MSE. Т.е. loss выглядит вот так:

$$

Код критика:

class CriticNetwork:
    def __init__(self):
        self.state_ph = tf.placeholder(tf.float32, shape=[None, observation_space])

        l1 = tf.layers.dense(self.state_ph, units=100, activation=tf.nn.tanh)        
        l2 = tf.layers.dense(l1, units=50, activation=tf.nn.tanh)
        l3 = tf.layers.dense(l2, units=25, activation=tf.nn.tanh)
        output = tf.layers.dense(l3, units=1)
        
        self.value_op = tf.squeeze(output, axis=-1)

        # Training
        self.value_ph = tf.placeholder(shape=[None], dtype=tf.float32)
        
        self.loss = tf.losses.mean_squared_error(self.value_ph, self.value_op)
        
        optimizer = tf.train.AdamOptimizer(learning_rate=critic_learning_rate)
        self.update_op = optimizer.minimize(self.loss)

Цикл обучения теперь выглядит так:

batch_generator = generate_batch(envs,
                                 batch_size=batch_size)

for epoch in tqdm_notebook(range(epochs_number)):
    batch = next(batch_generator)

    # Remainder: batch item consists of [state, action, value, reward-to-go]
    # Train actor
    _, actor_loss = sess.run([actor.update_op, actor.loss], 
                             feed_dict={actor.state_ph: batch[:, 0],
                                        actor.action_ph: batch[:, 1],
                                        actor.weight_ph: batch[:, 2]})
    
    # Train critic
    for j in range(10):
        _, critic_loss = sess.run([critic.update_op, critic.loss], 
                                  feed_dict={critic.state_ph: batch[:, 0],
                                             critic.value_ph: batch[:, 3]})

Теперь батчи содержат ещё одно значение, value, посчитанное критиком в генераторе.
Т.е. вид батча такой: $$.

В цикле ничто не ограничивает нас от обучения критика до сходимости, поэтому делаем несколько шагов градиентного спуска, тем самым улучшая аппроксимацию Value-функции и уменьшая bias. Однако такой подход требует большого размера батча, чтобы избежать переобучения. Аналогичное утверждение про обучение policy не верно. Она должна иметь моментальную обратную связь от среды для обучения, иначе мы можем оказаться в ситуации, когда мы штрафуем policy за действия, которые она бы уже совершать не стала. Алгоритмы с таким свойством называются on-policy.

Baselines in Policy Gradients

Можно показать, что в градиенте на место Value-функции допустимо ставить широкий класс других полезных функций от $$. Такие функции называются baselines. (Вывод этого факта) В качестве бейзлайнов хорошо себя показывают следующие функции:

Источник: GAE paper.

Разные бейзлайны дают разные результаты в зависимости от задачи. Наибольший профит как правило даёт Advantage-функция и её приближения.

За этим даже есть небольшая интуиция. Когда мы используем Advantage, мы штрафуем агента пропорционально тому, насколько лучше или хуже среднего сам агент считает совершённое им действие. И чем лучше агент играет в среде, тем выше становятся его стандарты. Идеальный агент будет хорошо играть и оценивать все свои действия как имеющие Advantage равный 0 и, следовательно, иметь градиент равный 0.

Оценка Advantage через Value-функцию

Напомним определение Advantage:

$$

Не понятно, как учить такую функцию явно. На помощь придёт трюк, который сведёт подсчёт Advantage-функции к подсчёту Value-функции.

Определим $$ — Temporal Difference residual (TD-residual). Не сложно вывести, что такая функция аппроксимирует Advantage:

$$

Такое концептуально сложное изменение провоцирует не такое большое изменение в коде. Теперь вместо оценки Value-функции критиком будем подавать на обучение policy оценку Advantage.

Полученный алгоритм называется Advantage Actor-Critic.

def estimate_advantage(states, rewards):
    values = sess.run(critic.value_op, feed_dict={critic.state_ph: states})
    deltas = rewards - values
    deltas = deltas + np.append(values[1:], np.array([0]))
    
    return deltas, values

У полученных агентов можно наблюдать уверенную походку и синхронное использование конечностей:

Generalized Advantage Estimation

Относительно недавно вышедшая статья (2018) "High-dimensional continuous control using generalized advantage estamation" предлагает ещё более эффективную оценку Advantage через Value-функцию. Она уменьшает variance ещё сильнее:

$$

где:

• $$ — TD-residual,
• $$ — discount-фактор (гиперпараметр),
• $$ — гиперпараметр.

Интерпретацию можно найти в самой публикации.

Реализация:

def discount_cumsum(x, coef):
    # Source: 
    # https://github.com/openai/spinningup/blob/master/spinup/algos/ppo/core.py
    """
    magic from rllab for computing discounted cumulative sums of vectors.
    input: 
        vector x, 
        [x0, 
         x1, 
         x2]
    output:
        [x0 + discount * x1 + discount^2 * x2,  
         x1 + discount * x2,
         x2]
    """
    return scipy.signal.lfilter([1], [1, float(-coef)], x[::-1], axis=0)[::-1]


def estimate_advantage(states, rewards):
    values = sess.run(critic.value_op, feed_dict={critic.state_ph: states})
    deltas = rewards - values
    deltas = deltas + discount_factor * np.append(values[1:], np.array([0]))
    
    advantage = discount_cumsum(deltas, coef=lambda_factor * discount_factor)
    return advantage, values

При использовании небольшого размера батча алгоритм сходился к некоторым локальным оптимумам. Здесь агент использует одну лапу как трость, а остальными отталкивается:

Здесь же агент не пришёл к использованию прыжков, а просто быстро перебирает конечностями. А также видно, как он ведёт себя, если запнётся — развернётся и продолжит бег:

Лучший агент, он же в самом начале статьи. Передвижение устойчивыми прыжками, во время которых от поверхности отрываются все конечности. Развитое умение балансировать позволяет агенту на полной скорости корректировать траекторию, если была допущена ошибка:

Подводные камни

Машинное обучение славится размерностью пространства ошибок, которые можно совершить, и получить полностью не работающий алгоритм. Но RL поднимает проблему на совершенно новый уровень.

Источник

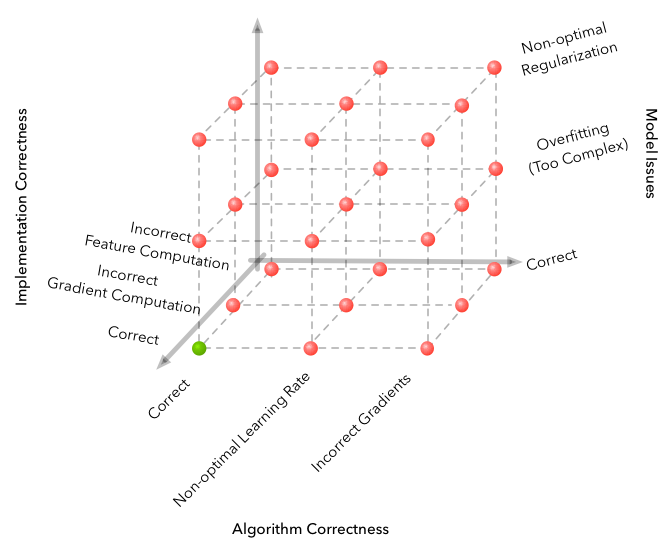
Здесь описаны некоторые трудности, с которыми пришлось столкнулся при разработке.

1. Алгоритм удивительно чувствителен к гиперпараметрам. Наблюдалось изменение в качестве обучения при смене learning rate с 3e-4 на 1e-4. И картина менялась радикально — с совсем не сходящегося алгоритма до лучшего, что есть в видео.
2. Размер батча совсем не такой, как в других областях DL. Если в image classification можно позволить себе выбрать размер батча 32-256 и результат особо не изменится от его увеличения, то здесь лучше взять несколько тысяч, для нашей задачи работает 3000. И снова от отсутствия сходимости до хорошего алгоритма.
3. Обучение лучше запускать несколько раз, иногда с random seed не везёт.
4. Обучение в такой довольно сложной среде занимает большое время, и прогресс не является равномерным. Например, лучший алгоритм обучался 8 часов, 3 из которых показывал результат хуже случайного бейзлайна. Поэтому при тестировании алгоритмов лучше начинать с малого вроде игрушечных сред из gym.
5. Хорошим подходом к поиску гиперпараметров и архитектур моделей будет подглядывать в реализации и статьи близкие по тематике. (главное не переобучаться)

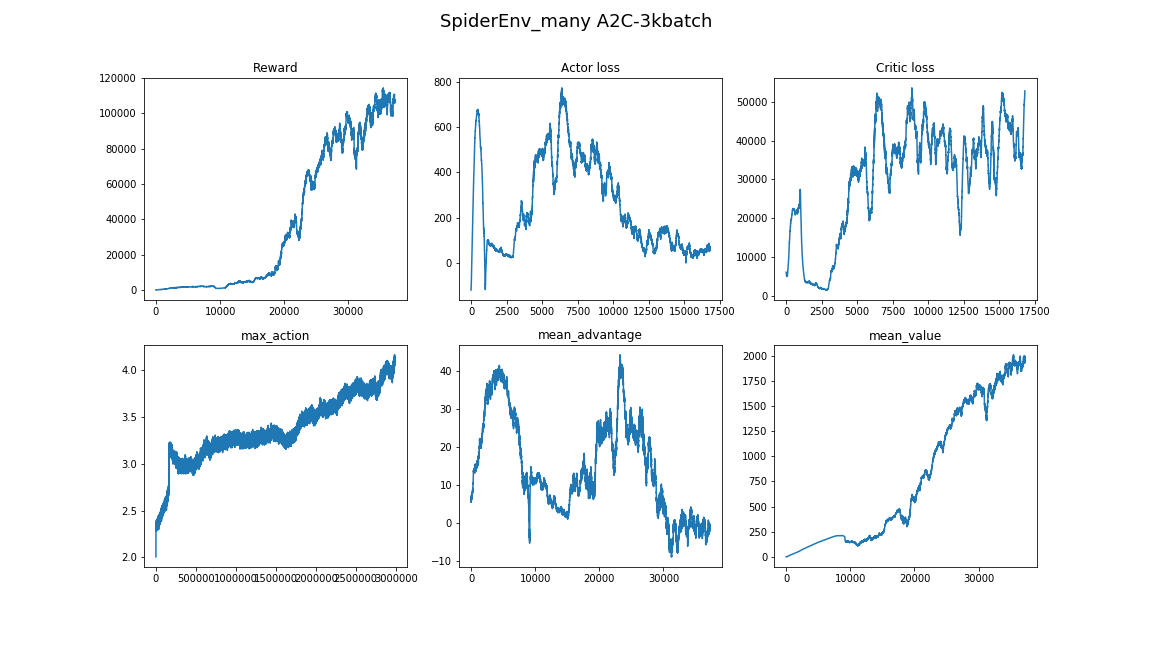
Больше нюансов в Deep RL можно узнать из этой статьи: Deep Reinforcement Learning Doesn't Work Yet.

Заключение

Получившийся алгоритм убедительно решает поставленную задачу. Найдена функция $$, проворно и уверенно управляющая роботом.

Логическим продолжением будет изучение близких родственников A2C, алгоритмов PPO и TRPO. Они улучшают sample efficiency, т.е. время сходимости алгоритма, и умеют решать более сложные задачи. Именно PPO + Automatic Domain Randomization недавно собрал Кубик Рубика на роботе.

Здесь можно найти код из статьи: репозиторий.

Надеюсь, вам понравилась статья и вы вдохновились тем, что уже сегодня умеет Deep Reinforcement Learning.

Спасибо за внимание!

Полезные ссылки:

• Welcome to Spinning Up in Deep RL!
• CS 294: Deep Reinforcement Learning, Fall 2017
• High-dimensional continuous control using generalized advantage estamation
• OpenAI Baselines: high-quality implementations of reinforcement learning algorithms

Спасибо pinkotter за помощь с проектом.