https://habr.com/en/post/481868/- JavaScript
- Game development
- Logic games
 It runs south and circles north, circling, circling to run with its wind
It runs south and circles north, circling, circling to run with its wind
And according to its circuits the wind returns;
All the rivers run into the sea — and the sea does not overflow,
To the place where the rivers run, — There they continue to run;
The book of Ecclesiastes
In 1998, a completely unique, for its time, application was developed that allows you to reduce the process of developing an abstract board game (or puzzle) to a small text description language, vaguely reminiscent of
Lisp. This project was called
Zillions of Games. It created a furor among fans of board games. Currently, over 2,000 applications have been created using this technology.
It quickly became clear that ZoG has many drawbacks. I already
wrote about this in Habr and I will not repeat myself. Let me just say that the developers did not take into account the features of a huge number of existing games and some important options were hard-coded, so that their change became extremely problematic. Greg Schmidt, in 2007, tried to rectify the situation by releasing the
Axiom Development Kit, but its tight integration with ZoG does not permit solving all the problems.
Project
Ludi pointed out new frontiers, using the universal game “engine” and
genetic algorithms to automate the process of development of new board games. Unfortunately, this approach was initially envisaged as a deliberate simplification of the game mechanics and of the level of the AI employed. Discussion of the goals of this project is beyond the scope of this article, but some of its technical solutions, no doubt, served as the starting point for my own development.
My goal is the development of a more versatile and user-friendly “engine” for the creation of abstract board games. For almost a year I have been studying the possibility of ZoG and Axiom and learned a great deal about their limitations. I think I can solve their problems by creating a more universal and cross-platform solution. On the progress of work on this project I shall report.
Openness and modularity
Perhaps the main drawback of ZoG is its closure. The product was assembled “once and forever” under one single platform — Windows. Were it open-source code, one could try to port it under Linux, Android, iOS … Another problem is its monolithicness.
In ZoG there are the beginnings of modularity, allowing for connection to the games DLL, including custom implementations of the AI. Axiom goes a little further, allowing you to run applications in the mode autoplay, without using the ZoG kernel. Notwithstanding the serious limitation of this solution (supporting applications only for two players), this example demonstrates how modularity would be helpful! The opportunity to organize a game with two bots (using different AI settings) and to collect statistics on a large number of games can not be overestimated. But how much better it would be if the product has been fully modular!
- Move generation module
- Move execution module
- Control module
- AI module
- Visualization module
All work describing the games is to be performed by the move generation module. This is the “heart” of the project. Transfer of all tasks not connected with this function to other modules will make it as simple as possible. You can improve this module, without looking at AI issues and user interaction. You can completely change the format of the description of games or add support for the descriptions in the format of ZoG, Axiom and Ludi. Modularity is the basis of flexibility of the solution!
The move execution module is the custodian of the game state. Information on the current game state is transferred to all other modules on demand. For reasons which I will give below, execution progress must pass through the generation module, whose task is the formation of a command in terms of module execution. Also, the task of the move generation module is the primary configuration of the game space, based on the description of the game.
The control module is, in fact, the application itself. It asks the move generation module for a list of possible moves and changes the game state, passing the selected move to the move execution module. The control module can be connected to play one or more AI bots. As many as you need (and possibly different)! The type of control unit is determined by the division of tasks. This may be autoplay to collect game statistics, game server (it can control several state stores, leading a large number of gaming sessions) or individual applications for playing offline.
The ability to connect different implementations of AI will improve the quality of the game. It is understood that the modules for the game of chess and Go should use different approaches. Games with incomplete information and games using random data also require an individual approach. Universal implementation of AI will be equally bad play all the games! Modular connection AI will allow to compare the “strength” of the algorithms, including a game mode “to each other.” Since the AI architecture is separated from the storage state of the game, one instance of the gaming bot can support an unlimited number of gaming sessions simultaneously.
Visualization of game process may also be varied. The first thing that comes to mind are 2D and 3D implementations. The platform for which the application is being developed, is also important. Less obvious is that visualization may be an important part of the game! For example, in the game
Surakarta, taking pieces will be completely non-obvious in the absence of proper animation of moves.
In general, modularity seems a good idea for such a project, and open source code will enable everyone who wishes to participate in the project. At the present time, I do not set myself commercial purposes, but I think that, if desired, I will find a way to make money without closing the source code.
The game space
Before starting the show, you need to set the stage. The board is not just a place where the pieces are arrayed. Beside that, the direction of movement of the pieces can be determined (in fact, the connections between the board positions) play areas (e.g., areas for conversion of pieces) forbidden fields, etc. Here is how the definition of the chess board looks in the ZoG-realization:
Defining the board in ZoG(define Board-Definitions
(image "images\Chess\SHaag\Chess8x8.bmp" "images\Chess\Chess8x8.bmp")
(grid
(start-rectangle 5 5 53 53)
(dimensions
("a/b/c/d/e/f/g/h" (49 0)) ; files
("8/7/6/5/4/3/2/1" (0 49)) ; ranks
)
(directions (n 0 -1) (e 1 0) (s 0 1) (w -1 0)
(ne 1 -1) (nw -1 -1) (se 1 1) (sw -1 1)
)
)
(symmetry Black (n s)(s n) (nw sw)(sw nw) (ne se)(se ne))
(zone
(name promotion-zone)
(players White)
(positions a8 b8 c8 d8 e8 f8 g8 h8)
)
(zone
(name promotion-zone)
(players Black)
(positions a1 b1 c1 d1 e1 f1 g1 h1)
)
(zone
(name third-rank)
(players White)
(positions a3 b3 c3 d3 e3 f3 g3 h3)
)
(zone
(name third-rank)
(players Black)
(positions a6 b6 c6 d6 e6 f6 g6 h6)
)
)
You may notice that besides the game settings, here are the settings associated with the visualization. I am firmly convinced that these settings do not belong here. In implementing a visualization module, multiple settings can be used and different settings may be required. Moreover, simulation games can work without any visualization module at all (like autoplay in Axiom). Indeed, since Axiom is used to visualize ZoG, the definition does not contain anything superfluous:
Defining the board in Axiom{board
8 8 {grid}
board}
{directions
-1 0 {direction} n
1 0 {direction} s
0 1 {direction} e
0 -1 {direction} w
-1 -1 {direction} nw
1 -1 {direction} sw
-1 1 {direction} ne
1 1 {direction} se
directions}
{symmetries
Black {symmetry} n s
Black {symmetry} nw sw
Black {symmetry} ne se
symmetries}
Unfortunately, Axiom also does not have a way to determe game zones (the location of game zones must be determined manually in the code). This is not Axiom's only simplification. Definition of the board in this project can not contain more than one grid and this grid must be two-dimensional. The board, thus defined, is a one-dimensional array, but for the convenience of the programmer, synonyms are defined for each of the spaces as follows:
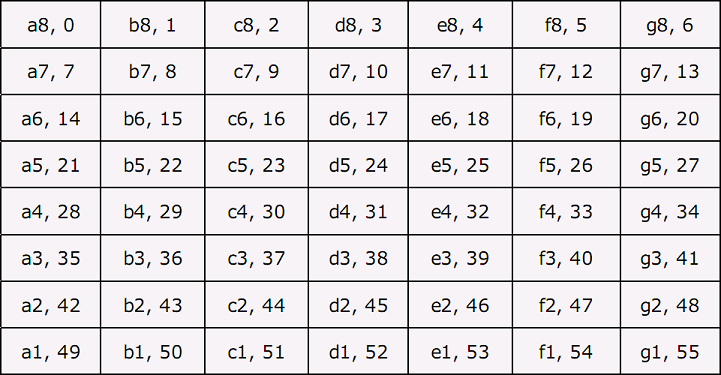
Compared with the more flexible scheme of grid definition in ZoG, these restrictions are quite uncomfortable (especially given the fact that the imposed naming scheme used these fields for the very purpose of visualization). Fortunately, it is possible to define a board of arbitrary shape. Both Axiom and ZoG provide an opportunity to identify element-wise each position on the board along with the ability to determine the links between arbitrary pairs of positions. Using this approach, we can define a board of any topology. Its only drawback is the extreme verbosity and complexity of the description.
In addition to the location of the pieces on the board and in the reserve, the system should have the ability to store attributes for individual pieces and for the spaces on the board. A good example of the need to use the attributes of a rule of “
castling” in
chess. This is a difficult move, which includes simultaneous movement of the king and a rook, allowed, provided that neither of these pieces have moved before performing this move. An attribute could be used to store a Boolean tag showing whether the piece has ever moved. Field attributes can also find some interesting applications.
It should be noted that attributes are not just variables but part of the game state. An attribute value may be changed by the execution of a turn (including by the AI module) and should be available for all subsequent turns, but not for turns performed in another branch of the game. Currently, ZoG supports storing boolean attributes of pieces. Axiom storage attributes are not supported, but you can add to the definition of the board a description of variables and arrays. These variables can be used, such as counters of the quantity of captured pieces:
{board
5 18 {grid}
{variable} WhitePieces
{variable} BlackPieces
board}
Yet another limitation of ZoG and of Axiom is the rule that each position of the board can contain no more than one piece. If any piece completes a move to a position occupied by another piece, the piece previously occupying the position is automatically considered to be “eaten”. This rule goes well with the “chess” principle of taking pieces and serves to simplify description of this game, but complicates the implementation of games such as “
bashni checkers” and “
tavreli”.
In these games, pieces can be arranged in “columns”. Such a “column” can be moved all together, as a single piece. After some reflection, I decided that it was better not to abandon the automatic implementation of the “Chess” capture, but to improve mechanisms for moving groups of pieces. Indeed, for the implementation of the “pillars”, you can always add to board another dimension (this is especially easy, as long as the visualization module is separated from the move generating module and from the AI, then you can use any logic whatsoever for rendering the three-dimensional board into its two-dimensional visualization). An additional argument in favor of this decision was that “high-stacked” movement of pieces is not the only type of group travel. For example, in “
Pentago” board fragments can be rotated together with the pieces mounted thereon.
Summarizing, I can say that, for my game framework, I decided to take all the best that has been thought up in ZoG, Axiom, and Ludi, and add whatever, in my opinion, they lack.
Move generation
Move generation is akin to
non-deterministic programming. The task of the move generator is providing, upon request, a list of all possible moves from the current position. Which move from this list will be selected by a player or AI is not its function. Let's see how the generation of moves is done in ZoG. As an example, we take the move generation macro for a long-range piece (a queen or bishop). This is how it is used in determining moves for these pieces:
(piece
(name Bishop)
(image White "images\Chess\SHaag\wbishop.bmp" "images\Chess\wbishop.bmp"
Black "images\Chess\SHaag\bbishop.bmp" "images\Chess\bbishop.bmp")
(moves
(slide ne)
(slide nw)
(slide se)
(slide sw)
)
)
As a parameter, a macro is passed the direction of movement on the board. If you do not consider the possibility of installing new pieces on the board, the generation of a move looks simple. For each of the pieces on the board, all possible moves according to the rules are calculated. Then the magic begins…
Each of the definitions can add to the list a number of possible moves! Adding a move to the list is done with the command add (at the same time positioning each moving piece on the board). I already
wrote about how this architectural solution is extremely poor. The command for the formation of the move should be separated from the commands that manipulate pieces (as was done in Axiom). Let's see how the macro works:
(define slide
( $1
(while empty?
add
$1
)
(verify not-friend?)
add
))
First, the displacement is performed by one cell, in the given direction, then in a cycle the space reached is checked for the absence of the pieces on it, a move is formed, and the arrangement proceeds to another cell in the same direction. If you stop here, the piece can “slide” through empty cells, but how can you take enemy pieces?
Very simple! Having run the command verify, the verication that the field is not occupied by a friendly piece, we form another add command, completing the move. If on this cell was located an enemy piece, it will be taken automatically (as on one space of the board, at one time, you cannot have more than one piece). If the piece was friendly, the calculation of the move will abort with the command verify (violation of the conditions specified in this command immediately terminates the calculation of the current move).
n both ZoG and Axiom one can move only one's own pieces (or rather, moving the opponent's pieces is possible, but only if specified in the mode of calculation of a move of one of one's own pieces). I find this an extremely inconvenient restriction, because there are many games in which you can directly move the opponent's piece (in “
Stavropol Checkers”, for example). It would be more consistent to perform the move calculation for all pieces, regardless of their affiliation. In the macro that determines the move, one would need only to add one check to allow moving only one's own pieces:
(define slide
( (verify friend?)
$1
(while empty?
add
$1
)
(verify not-friend?)
add
))
Important is the ability to perform a move consisting of several “partial” moves. In implementations of drafts, this ability is used to perform “chain” captures:
(define checker-jump
($1 (verify enemy?)
capture
$1
(verify empty?)
(if (not-in-zone? promotion-zone)
(add-partial jumptype)
else
(add-partial King jumptype)
)
)
)
The partial move command is formed with add-partial (for this command, as well as for the command add, there is a variation of the move, with “transformation” of the pieces). Such a move is always part of a larger, “composite” move. As a rule, for subsequent moves, a “mode” is set, which the continuation should implement. So in checkers, a capture can continue only with following captures but not with a “soft” (non-capturing) move.
NoteIn ZoG, implementation of partial moves is poor. Trying to execute the add-partial command in a cycle causes an error. As a result, the capture performed by a checker king can be realized only in the following very awkward manner:
(define king-jump-1
($1 (while empty?
$1
)
(verify enemy?)
capture
$1
(verify empty?)
(add-partial jumptype)
)
)
(define king-jump-2
($1 (while empty?
$1
)
(verify enemy?)
capture
$1
(verify empty?)
$1
(verify empty?)
(add-partial jumptype)
)
)
And so on, until king-jump-7! Let me remind you that in most varieties of checkers with a “long-range” king, the king, after each capture, can stop on any space of a continuous chain of empty spaces following the captured piece. There is, incidentally, one variant of this game in which the “chain” capture rule is formulated differently. That is just what I like about checkers — everyone can find a variant to one's liking.
Such a system of description of the rules is very flexible, but sometimes more complex logic is required. For example, if the piecee, during “partial” progress should not re-pass through a previously traversed field, it is logical to use the flags associated with positions on the board. Having visited a space, we set a flag, so subsequently not to go to this space again:
(verify (not-position-flag? my-flag))
(set-position-flag my-flag true)
In addition to “positional” flags, in ZoG you can use global flags. These capabilities should not be confused with the attributes of pieces. Unlike the latter, these are not part of the game state. Unfortunately, both attributes of pieces and flags in ZoG can only be boolean (in Axiom attributes are not even supported). This limitation makes it difficult to perform operations associated with the various types of counting. For example, in
this little puzzle, I had to use for “counting” pieces, caught in a “fork”, a pair of boolean flags (the exact number I did not need, as long as the pieces were more than one).
Another thing to fix is the lack of a clear “life cycle” in the execution of the move. All flags are automatically reset before starting the move, but it would be easier to identify clearly the initialization phase. In my opinion, in the calculation of the move, there should occur the following phases:
- Initialization of variables and checking preconditions for the composite move
- Initialization of variables and checking preconditions for the partial move
- Generation of the partial move
- Checking postconditions of the partial move
- Generating, completing, and checking postconditions of the composite move
- Checking for the termination conditions of the game
The group of steps from the second to the fourth, in the full composite move, may be repeated many times. The idea of pre- and post-conditions, which I call invariants, I took from the project Ludi. I tell you more about the use of invariants later.
On the importance of notation
Generation of all possible moves from the position is only half of the story. To control the game state requires a compact presentation of the generated moves. In ZoG, for this purpose, ZSG-notation is used. Here is an account of a possible beginning of a chess game in this form:
1. Pawn e2 - e4
1. Pawn e7 - e5
2. Knight g1 - f3
2. Knight b8 - c6
3. Bishop f1 - c4
3. Knight g8 - f6
4. King e1 - g1 Rook h1 - f1 @ f1 0 0 @ g1 0 0
4. Pawn d7 - d5
5. Pawn e4 x d5
5. Knight f6 x d5
This script is close to the usual
chess notation and generally user friendly. Only white's fourth move may cause some confusion. So in ZSG it looks like
castling. The part of the description of the move before the '@' character is quite clear; it is the simultaneous movement of the rook and the king, but what follows? Thus, in ZSG, it looks like a reset of attributes of the pieces is required in order to prevent the possibility of repeated castling.
NoteZoG uses its ZSG-notation particularly in order to show the course of the game in a form understandable to the player. On the right of the board, a «Moves List» sub-window may be open. This list can be used to navigate through the recorded game. This list is not very convenient, because a branching tree view of alternative games is not supported. The part of the recorded turns associated with changes in attributes of pieces, is not displayed to the user.
The recording of a move in ZSG-notation should contain full information sufficient to correctly change the game state. If information about a change of attributes is lost, in a game according to such a record, a move could be incorrectly repeated (for example, the player would have the opportunity to re-execute the castling). Unfortunately, in DLL-extensions (such as Axiom), extended information can not be transmitted.
Working with DLL-extensions, ZoG is forced to make a quite cunning manipulation when positioning to a selected move (for example, when you roll back a move). From [each] previous position [working from the beginning of the game], all possible moves are generated, and then, within that list, one must search for a move with the [corresponding] ZSG representation. The [side effects of each] generated move is are applied to [each successive] game state, as it is possible to perform side-effects not reflected in the move's ZSG-representation.
The situation is aggravated by the fact that the only way to get to the game state at the time of a move in the past, is the consistent application of all the moves from the beginning of the game, to the initial state of the board. In really
complex cases, this kind of navigation does not occur quickly. Another disadvantage of ZSG-notation can be illustrated by the recording of the following move in the game of
Go:
1. White Stone G19 x A19 x B19 x C19 x D19 x E19 x F19
Here, in the position G19, a white stone is placed that captures a group of black stones. Since all the pieces involved in the performance of the placement must be mentioned in the ZSG-performance, the record of the turn may seem very long (in Go, one drop may capture up to 360 stones). To what this may lead, I wrote
earlier. The buffer size allocated for recording the ZoG move, may not be enough. Moreover, if for some reason the order of removal of stones changes (in the process of development of the game it happens), an attempt to apply a move, from an old order of captures, will fail.
Fortunately, there is a simple way to deal with all these problems. Let's look at how to define moves of pieces in ZRF:
(piece
(name Pawn)
(image White "images\Chess\SHaag\wpawn.bmp" "images\Chess\wpawn.bmp"
Black "images\Chess\SHaag\bpawn.bmp" "images\Chess\bpawn.bmp")
(moves
(Pawn-capture nw)
(Pawn-capture ne)
(Pawn-move)
(En-Passant e)
(En-Passant w)
)
)
Names of moves, defined in ZoG macros, are inaccessible as a generator of moves. But what prevents us from giving up on macros and making descriptions of the moves with their names? Here's how the record would look for a chess game:
1. e2 - e4 Pawn-move
1. e7 - e5 Pawn-move
2. g1 - f3 leap2 n nw
2. b8 - c6 leap2 n ne
3. f1 - c4 slide nw
3. g8 - f6 leap2 n nw
4. e1 - g1 O-O
4. d7 - d5 Pawn-move
5. e4 x d5 Pawn-capture nw
5. f6 x d5 leap2 w nw
NoteAstute readers may notice that in the moves for “black” I used directions not appropriate to the actual directions on the chessboard. This is connected with the fact that “symmetries” are defined for black:
(symmetry Black (n s)(s n) (nw sw)(sw nw) (ne se)(se ne))
Roughly speaking, then, what for white is “north”, for black is “south”, and vice versa.
The benefits of such a record is not obvious, but it has one important advantage. All moves are described in a uniform manner and these descriptions do not contain anything extra (the names of descriptions of moves, of course, could be made more “descriptive”). In the description of castling one managed to get rid of both the changes of attributes and of the description of the rook move (this description is no longer dependent on the implementation details of the move). An even clearer usefulness of such records exists in the case of the game of Go:
1. G19 drop-to-empty White Stone
And that's it! If the opponent's stones are taken in accordance with the rules of the game, there is no need to list them all in the move description. It is sufficient to indicate the initial and final space of displacement (possibly with a sign to take), the name of the executing move and the line of parameters passed to it. Of course, in order to perform a move according to this description, for decoding, it is necessary to access the move generation module, but ZoG does so!
Another possibility, which one should support, appears in the functionality of “partial” moves. Here is an example from “
Russian checkers”:
1. Checker g3 - f4
1. Checker f6 - g5
2. Checker e3 - d4
2. partial 2 Checker g5 - e3 = XChecker on f4
2. Checker e3 - c5 = XChecker on d4 x d4 x f4
Here the blacks, on their second move, take two pieces on d4 and f4. A preliminary “transformation” of these pieces to XChecker is a feature of this implementation and serves to prevent the re-taking of “defeated” pieces on the same move. The phrase “partial 2” describes the beginning of “composite” course, which consists of two “partial” moves. This form of description is inconvenient, because at the time of generation of the first move, the length of the sequence of “partial” moves may not be known. Here's how this description will look in a new format:
1. g3 - f4 checker-shift nw
1. f6 - g5 checker-shift ne
2. e3 - d4 checker-shift nw
2. + g5 - e3 checker-jump nw
2. + e3 - c5 checker-jump sw
2. +
Implementation details related to the “transformation” of pieces are irrelevant. The capture of pieces is also not specified, as in checkers, capture occurs as a “side effect” of the piece's move and not according to the “principle of chess.” Partial progress will be encoded with the symbol “+” at the beginning of the line. A lone “+” indicates the completion of a “composite move” (in fact, this is the usual “partial” move, containing a missing move, an empty string).
Thus, using named rules for the implementation of moves, one has managed to create a universal notation, fully satisfying our requirements. Of course, it has nothing to do with either the standard chess or with any other notation, but it just so happens that the conventional notation for chess, checkers and other games, too, have nothing to do with each other. The visualization module can always convert the move record into a more familiar form accepted for a particular game. Conversion can also be into some universal form, like
SGF (Smart Game Format).
The life cycle of the game
In addition to information about placing pieces on the board, the sequence of turns is a compnent part of the game state, a variable in the game process. In the simplest (and most common) case, for storing this information one bit will suffice, but ZoG provides a few more opportunities to implement more complex cases. Here is how a description of a sequence of moves could look for the game
Splut!:
(players South West North East)
(turn-order
South
West West
repeat
North North North
East East East
South South South
West West West
)
In this game, each player makes three moves at a time, but if you were to give the first player the opportunity to make three moves from the initial position, he would be able to destroy one of the opponent's pieces, which would give him a significant advantage. For this reason, the first player should make only one move (it gives an opportunity to prepare to attack an opposing player, but not attack him), the second — two moves (this is also not enough to attack an opposing player), after which each player always makes three moves.

The label repeat indicates the beginning of a cyclically repeating sequence of moves. If it does not appear, the entire description is repeated cyclicly. ZoG does not allow the use of the label repeat more than once. Another important feature is the specification of the turn order. Here's how a description of the sequence of turns for a game in which each player performs two turns (the first move — moving pieces, the second — capturing opponent's pieces) might look:
(players White Black)
(turn-order
(White normal-move)
(White capture-move)
(Black normal-move)
(Black capture-move)
)
There is one more capability associated with the description of moving someone else's pieces, but it is very inconvenient to use. The problem is that such a description has no alternative. If the description states that the move should be done by an enemy piece, the player must perform this move! In ZoG it is impossible to describe a choice of moving his own or someone else's piece. If such an capability is needed in a game (such as in “
Stavropol Checkers”), it is necessary to make all the pieces neutral (creating for this purpose a player who does not participate in the game) and determine for all players the opportunity to move a neutral piece. I have said above that it is much easier by default to allow all players the ability to move any pieces (their own as well as their opponent's) adding the necessary checks in the move generation algorithms.
As you can see, the range of options provided by ZoG for description of the sequence of turns is extremely limited. Axiom also fails to add new features, because it (usually) runs over ZoG. Ludi, in this respect, is even poorer. In order to maximize unification of the rules of the game (required for the possibility of using generic algorithms), in this project, all descriptive capabilities have been deliberately simplified, which has brought about an elimination of whole layers of games.
"
Bao Swahili” is a good example of a game with a complex life cycle. In this game, the are two phases with rules for move execution which differ significantly. At the beginning of the game, part of the stones is “in the hand” of each player. While there are still stones “in hand”, stones are put into wells, one stone at a time. When the stones “in hand” run out, the second phase of the game begins, with the distribution of inserted stones. One cannot say that this game can not be described in ZRF (the description language of ZoG), but because of the limitations of ZoG, this implementation would be extremely confusing (which certainly is not best for the quality of AI work). Let's see how the description of such a game would look in an “ideal world”:
(players South North)
(turn-order
(turn-order
(South p-i-move)
(North p-i-move)
)
(label phase-ii)
(turn-order
(South p-ii-move)
(North p-ii-move)
)
)
Here, each turn-order list determines its repeating sequence of moves (distinguishing itself by mode of move execution). The keyword label defines a label to which a transition can be made during the generation of the latest move. You may notice that here we proceed from the implicit assumption that such a transition always occurs after the move of the second player (otherwise it would violate the sequence of moves). How to make the transition to the next phase at an arbitrary time?
(players South North)
(turn-order
(turn-order
(South p-i-move)
(North p-i-move)
)
(turn-order
(labels - phase-ii)
(South p-ii-move)
(labels phase-ii -)
(North p-ii-move)
)
)
Here, labels are carried in the loop body and comprise two names. Label names in the labels lists appear in the order of transfer of players in the list of players. The name used for the transition is determined by which player made the last move. If this was the North, it will transition to the first label, otherwise, to the second. If any of the names in the labels will not be used, the corresponding position can be filled by a dash.
An important aspect in the management of alternating moves, is the ability to perform a repeated turn. In games of the
Tables family, such as
Nard,
Backgammon, or
Ur, for example, the ability to perform repeated turns is an important element of game tactics. In ZoG one can use passing a turn to emulate this feature, but this approach significantly complicates the description of the game (especially with more players). It would be much more logical to use a label for repeating a turn:
(players South North)
(turn-order
(label repeat)
South
(label repeat)
North
)
The game having jumped to the label repeat, the player will again play his turn (the label closest to the current position in the list of turns will take effect). I like the approach of
Perl in its implicit definitions. Implicit generation of control structures can significantly simplify game description. Inasmuch as repeated moves can be used in many games, the labels repeat, anticipating possible repetion of any turn can be implicit:
(players South North)
(turn-order
South
North
)
Moreover, since the sequence of turns is fully consistent with the written order of players in the players construct, you can automatically generate the entire turn-order phrase:
(players South North)
The easier the description is to write, the better.
Breakable invariant
The main thing that I do not like in ZoG can be expressed with one word — checkmated. At first glance, it's just a condition (very common in games of the
chess family) linking the end of the game with the formation a mate situation. Alas, on closer examination, the simplicity shows itself to be deceptive. Use of this keyword means not only the performance, after each move, of a check for the completion of the game, but also imposes upon the player certain “behavior”.
From the usual
Shogi, this game differs only in the number of players. Unfortunately, this difference is enough to make the job of determining checkmate (and everything associated with this “magic” word) incorrect. Verifying being in check is performed only with relation to one of the players. As a result, the king may come to be under attack, and be eaten [by a combination of opponents' turns even when not left in “check”]! That this is not optimal will be reflected in the work of the AI.
If this problem seems insignificant, it is worth remembering coalitions are usually formed in four-player games “pair against pair”. In the case of the formation of coalitions, we must consider that pieces friendly to the king do not threaten him! So, for example, two friendly Kings may well reside on neighboring spaces of the board.
It becomes more complicated than ever if a player may have several kings. In “
Tamerlane chess”, the royal pawn turns into a prince (actually, a second king). If this happens, you can win only by capturing the first king (either of the two), and mating the second. In this game, you can get even a third king, double spending on the transformation of the “pawn of pawns”! The expressive capabilities of “checkmated” are not enough to adequately describe this situation.
Another difficulty may be the very process of giving mate. So in Mongolian chess (
Shatar), the result of attempted mate depends on the order in which the pieces execute sequential “check”. The result can prove to be either win or a draw (such as mate by a pawn), or even a defeat (horse mate forbidden, but you can give check). Slightly less exotic, in this regard, is Japanese Shogi. In this game, it is forbidden to give mate with a dropped pawn, but you can give check with a dropped pawn and give check mate with a moved pawn.
NoteThere is one more important point worth mentioning. In some games, such as Rhythmomagic, there can be several different ways to end the game. The most obvious way to win, involving the destruction of the opponent's pieces, is also the least preferred. For more significant victory, one must arrange one's pieces on enemy territory in a certain pattern.
One should distinguish between the types of victories (and defeats and draws) at the level of game description, since the type of game ending may matter to the player. In addition, it should be possible to assign numerical priorities to the various game endings. Upon simultaneous fulfillment several completion conditions, the one that has the highest priority should count.
Obviously, one must separate the logic of verification of game end from the test for the king's having fallen into check, which is an
invariable rule that is checked after each turn. Violation of the rule makes it impossible to perform the move (the move is removed from the list of available moves). So a (simplified) test for a King's being in check might look like this for “Tamerlane chess”:
(verify
(or
(> (count (pieces my? (is-piece? King))) 1)
(= (count (pieces my? (is-piece? King) is-attacked?)) 0)
)
)
It is important to understand that this test should be carried out only for one's own kings (I used the predicate my?, because the predicate friend?, with support for coalitions, will be satisfied not only for one's own pieces, but also for the pieces of all friendly players). Acceptable (and desirable, [if there are multiple friendly kings]) is the situation in which the enemy king falls under check, after a move, but by one's own king. This situation should be impossible [unless there are multiple friendly kings]! Having provided support for checking such rules, checking for the completion of the game by checkmate becomes trivial. If there are no possible moves and the [only] king is in check, the game is over [if that king belongs to the last surviving player of the second last surviving coalition]:
(loss-condition
(and
(= (count moves) 0)
(= (count (pieces my? (is-piece? King)) 1)
(> (count (pieces my? (is-piece? King) is-attacked?)) 0)
)
)
The ability to determine invariants will be useful in other games, such as in
checkers. The greatest difficulty in the implementation of games of this family, is linked to the implementation of the “majority rule”. In almost all drafts games, capturing is compulsory. Also, in most games of this family, there is a characteristic completion of “chain captures” in a single turn. The checker, having captured, continues to take other pieces, if possible. In most games, the player is required to carry out chain captures to the end, but there are exceptions to this rule, for example,
Fanorona.
Using the mechanism of partial moves, implementating a “chain capture” is quite simple. Difficulties arise when, in addition, one imposes a condition under which, of all the possible options, one must choose a chain in which a maximal number of pieces are captured. In ZoG this logic must be implemented from scratch at the level of “hardcoding”:
(option "maximal captures" true)
This setting is suitable for “
International checkers”, but in the “
Italian checkers” the majority rule is formulated differently. In this version of the game, if there are several options for the same number of captures, you must select an option which captures the larger number of transformed checkers (kings). The developers of ZoG have provided this. You enter the following setting:
(option "maximal captures" 2)
In this setting, one counts not only the number of pieces captured, but also their type. Unfortunately, not everything can be foreseen. Here's how the “majority rule” is formulated in “old French checkers”:
If by a series of captures it is possible to capture the same number of checkers with a simple man or with a king, the player must use the king. However, if the number of checkers is the same in both cases, but in one there is an enemy king (or there are more), the player must choose this option, even if the capturing is then done using the simple checker, and not using the king.
Of course, at the present time, almost no one plays this version of checkers, but its very existence clearly demonstrates the shortcomings of “hardcoded” implementation. Using the mechanism of invariants allows for all possible options for the “majority rule” in a universal manner. For the “
old French checkers” implementation would be as follows:
(verify
(>= capturing-count max-capturing-count)
)
(if (> capturing-count max-capturing-count)
(let max-capturing-count capturing-count)
(let max-capturing-sum capturing-sum)
(let max-attacking-value attacking-value)
)
(verify
(>= capturing-sum max-capturing-sum)
)
(if (> capturing-sum max-capturing-sum)
(let max-capturing-sum capturing-sum)
(let max-attacking-value attacking-value)
)
(verify
(>= attacking-value max-attacking-value)
)
(let max-attacking-value attacking-value)
Here, we assume that the rules for capture generation correctly fill [the following] local variables:
- capturing-count — total pieces captured
- capturing-sum — number of kings captured
- attacking-value — value of piece capturing
Associated with each of these variables is a value-accumulator, stored in a variable with the prefix max. The three checks are executed serially. Violation of any of the verify conditions immediately interrupts the generation of the next turn option (the capture is not stored in the list of possible turns). Since the checks performed are associated with variable values, it is not sufficient [to test only the current new capture option]. Each test generates a “bendable rule” associated with the generated capture [which may revise the accumulated maximum value]. After each change in any accumulator, all associated rules must be checked again [for every option in the list]. If any of the conditions are breached for a previously generated option, that option must be removed from the list of possible turn options.
Conclusion
This is translation of my article of 2014 year. Since then, I have rethought a lot and the
Dagaz project has become a reality, but I did not change almost anything in the text. This article was translated by my friend
Howard McCay and I am grateful to him for the work done.
 It runs south and circles north, circling, circling to run with its wind
It runs south and circles north, circling, circling to run with its wind





