Всем привет! Меня зовут Борис, я выпускник программы “Науки о данных” ФКН ВШЭ, работаю ML Инженером и преподаю в OTUS на курсах ML Professional, DL Basic, Computer Vision.
В первых числах января 2021 я узнал про “британский” штамм коронавируса, прогнозы о новой волне в США. Я подумал: “аналитик данных я или кто”? Мне захотелось забить гвоздик своим микроскопом и узнать, вызовет ли “британский” штамм волну заражений в Москве и стоит ли покупать авиабилеты на лето.
Выглядело как приключение на две недели, но превратилось в исследование на три месяца. В процессе я выяснил, что хороших материалов по созданию эпидемиологических моделей практически нет. Банально авторы статей по моделированию COVID-19 в топовых журналах даже не делают train-test split.
Я предлагаю туториал на основе своего исследования. В нём я постарался передать все важные детали, которые сэкономили бы мне много недель, если бы о них кто-то писал.
COVID-19 в представлении не нуждается, к нему мы уже привыкли. Однако новые мутации (штаммы) вируса способны изменить ход эпидемии. Сейчас ВОЗ выделяет три таких штамма (variants of concern). Среди них штамм B.1.1.7, так называемый “британский” штамм.
Почему меня заинтересовал именно он? Во-первых, исследования показывают, что этот штамм распространяется на 40% - 90% быстрее, чем обычный коронавирус (для продвинутых: R0 на 40% - 90% больше). Во-вторых, случай заражения этим штаммом уже был обнаружен в России. В-третьих, непохоже, чтобы кто-то в России готовился к его появлению.
По результатам исследования пришел к выводу, что B.1.1.7 действительно способен привести к новой волне заражений COVID-19 и может унести 30 тысяч жизней.
Исходные данные
Нам понадобится статистика по заражениям, смертям и выздоровлениям в Москве. Её можно скачать со страницы. На момент исследования был доступен промежуток дат: 2020.03.10 - 2021.03.23.
Изначально данные даны для всей России. Модель, которую мы будем использовать, работает лучше для замкнутых популяций, так что ограничимся моделированием для Москвы. Кроме того поправим индексы и переименуем колонки.
Добавим сглаженные скользящим окном в 7 дней версии всех колонок. Они пригодятся нам позже.
df_smoothed = df.rolling(7).mean().round(5)
df_smoothed.columns = [col + '_ma7' for col in df_smoothed.columns]
full_df = pd.concat([df, df_smoothed], axis=1)
for column in full_df.columns:
if column.endswith('_ma7'):
original_column = column.strip('_ma7')
full_df[column] = full_df[column].fillna(full_df[original_column])
В итоге работаем со следующими колонками, а так же их сглаженными версиями:
infected_per_day — новых заражений в данный день.
recovered_per_day — новых выздоровлений в данный день.
deaths_per_day — погибших от инфекции в данный день.
total_infected — всего заражений к этому моменту, кумулятивная сумма infected_per_day.
total_dead — всего погибших к этому моменту, кумулятивная сумма от deaths_per_day.
total_recovered — всего выздоровлений к этому моменту, кумулятивная сумма от recovered_per_day.
Основа модели: SEIRD
SIR это очень простая модель, которая симулирует развитие эпидемии во времени. Популяция разделяется на три группы: Susceptible, Infected, Recovered. Идея “на пальцах”:
Есть замкнутая популяция и изначальное количество зараженных (Infected).
В течение дня каждый зараженный с некоторой вероятностью инфицирует кого-то из группы Susceptible. Новые зараженные переходят в группу Infected.
Находящиеся в группе Infected выздоравливают, когда проходит срок длительности болезни и переходят в группу Recovered.
Запускаем этот процесс на много дней вперед и смотрим, как меняется численность групп.
SIR не учитывает наличие инкубационного периода и погибших, так что сразу перейдем к расширению SEIRD и рассмотрим его подробнее. SEIRD работает точно так же, но разделяет популяцию на следующие группы:
Susceptible — могут быть заражены.
Exposed — заражены вирусом, но не распространяют его, то есть проходят инкубационный период.
Infectious — распространяют вирус.
Recovered — переболели и не могут быть заражены.
Dead — погибли.
Изменение численности групп за день определяют дифференциальные уравнения:
Например, третье уравнение описывает изменение группы Infected за день. С вероятностью δ у человека из группы E заканчивается инкубационный период и он переходит в группу I. Так же с вероятностью γ человек из группы I выздоравливает или погибает, переходя в группу R или D. Куда он попадет определяется параметром α, который соответствует доле смертности (Infection Fatality Rate). Таким образом, каждый день группу пополняют новые зараженные, а переболевшие уходят из группы.
Параметры модели: α — case fatality rate. β — количество человек, которых один переносчик заражает за день. δ — 1 делить на среднюю длину инкубационного периода. y — 1 делить на среднюю длительность болезни. R0 = β/y — базовое репродуктивное число, то есть количество человек, которых один переносчик заражает за время своей болезни.
Есть три причины использовать именно SEIRD. Во-первых, параметры SEIRD это просто характеристики болезни, а значит мы сможем прикинуть их значения на основании медицинских исследований COVID-19 как болезни. Во-вторых, эту модель очень легко модифицировать, что мы и будем делать дальше, добавляя меры карантина, неполноту статистики и второй штамм. В-третьих, эта модель позволяет легко “покрутить” разные сценарии. Например, можно смоделировать ситуацию: “Что будет, если в этой же популяции появится второй штамм и параметр R0 у него на 90% больше?” Сделать подобное с помощью, например, градиентного бустинга, гораздо сложнее.
Главный минус SEIRD: это очень простая и полностью детерминированная модель. Она чувствительна к изначальным значениям и параметрам. Предсказания такой модели могут на порядки отличаться от реальных значений. Для нас это не страшно: мы ведь не пытаемся сделать самый точный прогноз по количеству зараженных, мы просто пытаемся понять может ли штамм B.1.1.7 вызвать новую волну. Интересно, что, несмотря на это, лучшая на текущий момент модель по прогнозированию COVID-19 это очень навороченная SEIR модель.
Реализуем классический SEIRD
Привожу минимальную реализацию SEIRD.
class BarebonesSEIR:
def __init__(self, params=None):
self.params = params
def get_fit_params(self):
params = lmfit.Parameters()
params.add("population", value=12_000_000, vary=False)
params.add("epidemic_started_days_ago", value=10, vary=False)
params.add("r0", value=4, min=3, max=5, vary=True)
params.add("alpha", value=0.0064, min=0.005, max=0.0078, vary=True) # CFR
params.add("delta", value=1/3, min=1/14, max=1/2, vary=True) # E -> I rate
params.add("gamma", value=1/9, min=1/14, max=1/7, vary=True) # I -> R rate
params.add("rho", expr='gamma', vary=False) # I -> D rate
return params
def get_initial_conditions(self, data):
# Simulate such initial params as to obtain as many deaths as in data
population = self.params['population']
epidemic_started_days_ago = self.params['epidemic_started_days_ago']
t = np.arange(epidemic_started_days_ago)
(S, E, I, R, D) = self.predict(t, (population - 1, 0, 1, 0, 0))
I0 = I[-1]
E0 = E[-1]
Rec0 = R[-1]
D0 = D[-1]
S0 = S[-1]
return (S0, E0, I0, Rec0, D0)
def step(self, initial_conditions, t):
population = self.params['population']
delta = self.params['delta']
gamma = self.params['gamma']
alpha = self.params['alpha']
rho = self.params['rho']
rt = self.params['r0'].value
beta = rt * gamma
S, E, I, R, D = initial_conditions
new_exposed = beta * I * (S / population)
new_infected = delta * E
new_dead = alpha * rho * I
new_recovered = gamma * (1 - alpha) * I
dSdt = -new_exposed
dEdt = new_exposed - new_infected
dIdt = new_infected - new_recovered - new_dead
dRdt = new_recovered
dDdt = new_dead
assert S + E + I + R + D - population <= 1e10
assert dSdt + dIdt + dEdt + dRdt + dDdt <= 1e10
return dSdt, dEdt, dIdt, dRdt, dDdt
def predict(self, t_range, initial_conditions):
ret = odeint(self.step, initial_conditions, t_range)
return ret.T
Давайте разберемся.
Метод get_fit_params просто создает хранилище парамтеров. Мы используем библиотеку lmfit, но пока что не оптимизируем параметры, а просто используем структуру Parameters как продвинутый словарь. Для задания диапазонов параметров я использовал мета-анализы характеристик COVID-19.
Параметр epidemic_started_days_ago позволяет задать дату появления первого зараженного. В моём предположении это 2 марта 2020.
Метод step содержит дифференциальные уравнения модели. Он получает на вход изначальные численности всех групп в виде кортежа initial_conditions и номер дня t, возвращает изменения всех групп за день.
Метод predict получает на вход начальные условия и массив t_range. Он просто запускает scipy.integrate.odeint на методе step, чтобы проинтегрировать дифференциальные уравнения и получить численность групп в каждый день из массива t_range.
Метод get_initial_conditions запускает модель с момента появления первого зараженнного на epidemic_started_days_ago дней и возвращает полученные численности групп. Далее эти численности используются как начальные значения для моделирования последующих дней.
Запустим модель и сравним её предсказания с реальностью:
Модель предсказывает, что все уже умерли или переболели, а эпидемия давно закончилась. Результат ужасный, но ожидаемый.
Взглянем на динамику всех групп SEIRD:
Модель описывает одну “волну” заражений, после которой почти все выздоравливают, достигается групповой иммунитет и эпидемия сходит на нет. Даже если мы подберем самые лучшие параметры, эта модель просто не способна описать несколько “волн” эпидемии. Нам необходимо изменить систему уравнений, чтобы получить более полезный результат.
Добавляем сдерживающие меры
Одна из причин появления нескольких “волн” это сдерживающие меры. Предположим, что карантинные меры в день t, снижают R0 болезни на процент q(t). Тогда для каждого дня можно расчитать репродуктивное число с учетом карантина: Rt = R0 - R0 * q(t). Отсюда мы можем вычислить β(t) = Rt * y и использовать её в уравнениях.
Осталось только задать функции q(t). В своём исследовании я использовал простую ступенчатую функцию. Делим весь промежуток на отрезки по 60 дней, для каждого отрезка добавляем новый параметр: уровень карантина в данный период. Переходы между отрезками стоит сделать плавными с помощью, иначе функция не будет гладкой и подбирать параметры будет сложно.
Реализуем небольшой пример для наглядности.
def sigmoid(x, xmin, xmax, a, b, c, r):
x_scaled = (x - xmin) / (xmax - xmin)
out = (a * np.exp(c * r) + b * np.exp(r * x_scaled)) / (np.exp(c * r) + np.exp(x_scaled * r))
return out
def stepwise_soft(t, coefficients, r=20, c=0.5):
t_arr = np.array(list(coefficients.keys()))
min_index = np.min(t_arr)
max_index = np.max(t_arr)
if t <= min_index:
return coefficients[min_index]
elif t >= max_index:
return coefficients[max_index]
else:
index = np.min(t_arr[t_arr >= t])
if len(t_arr[t_arr < index]) == 0:
return coefficients[index]
prev_index = np.max(t_arr[t_arr < index])
# sigmoid smoothing
q0, q1 = coefficients[prev_index], coefficients[index]
out = sigmoid(t, prev_index, index, q0, q1, c, r)
return out
t_range = np.arange(100)
coefficients = {
0: 0,
30: 0.5,
60: 1,
100: 0.4,
}
plt.title('Пример функции уровня карантина')
plt.scatter(coefficients.keys(), coefficients.values(), label='Моменты изменения уровня карантина')
plt.plot(t_range, [stepwise_soft(t, coefficients, r=20, c=0.5) for t in t_range], label='Ступенчатая функция с плавными переходами')
plt.xlabel('t')
plt.ylabel('Уровень канартина')
plt.legend(loc='lower center', bbox_to_anchor=(0.5, -0.6),)
plt.show()
Чтобы добавить это в нашу SEIRD модель нужно сделать несколько шагов:
Добавляем мультипликаторы карантина в get_fit_params. Изначально карантин находится на уровне нуля, но для остальных отрезков его уровень будет определен оптимизацией. Так же появляется новый гиперпараметр, задающий длину отрезков: stepwise_size, по умолчанию 60 дней.
def get_fit_params(self, data):
...
params.add(f"t0_q", value=0, min=0, max=0.99, brute_step=0.1, vary=False)
piece_size = self.stepwise_size
for t in range(piece_size, len(data), piece_size):
params.add(f"t{t}_q", value=0.5, min=0, max=0.99, brute_step=0.1, vary=True)
return params
Добавляем новый методget_step_rt_beta, который вычисляет β(t) и Rt используя ступенчатую функцию.
В методе step используем get_step_rt_beta, β(t) с учетом карантина в день t.
Учитываем неполноту статистики
Известно, что не все случаи заражения попадают в официальную статистику. Многие люди просто не обращаются в больницы, а часть болеет безсимптомно. Мы можем учесть это в нашей модели.
Изменим группы Infected, Recovered и Dead следующим образом:
Iv(t) — распространяют вирус, видны в статистике.
I(t) — распространяют вирус, не видны в статистике.
Rv(t) — переболели, видны в статистике.
R(t) — переболели, не видны в статистике.
Dv(t) — погибли, видны в статистике.
D(t) — погибли, не видны в статистике.
Добавим два новых параметра:
pi — вероятность попадания зараженного в статистику, то есть в группу Iv.
pd — вероятность регистрации смерти зараженного, невидимого в статистике, в группу Dv. Зараженные из группы Iv всегда попадают в Dv, но этот параметр позволяет учесть, что часть смертей незамеченных зараженных так же попадает в статистику по смертности от COVID-19.
В конце концов мы приходим к такой схеме модели, где вершины графа это группы, а стрелки определяют как люди перемещаются между группами:
Для удобства будем называть её SEIRD со скрытыми состояниями. Она отличается от обычного SEIRD только дифференциальными уравнениями. Подробности реализации можно посмотреть здесь.
Оптимизируем параметры
Модель готова, осталось только подобрать оптимальные значения параметров так, чтобы выдаваемые моделью Iv(t), Rv(t) и Dv(t) были как можно ближе к историческим данным. Это можно сделать с помощью метода наименьших квадратов.
Конкретнее, используем для этого lmfit.minimize. Эта функция получает на вход callable, возвращающий список отклонений предсказаний от истины (остатки, residuals), и подбирает такие параметры, чтобы сумма отклонений была минимальна. Используем алгоритм Levenberg-Marquardt (method=’leastsq’), который двигает каждый параметр на очень маленькое значение и проверяет, уменьшается ли ошибка. Важно знать, что по этой причине алгоритм не может оптимизировать дискретные параметры, поэтому, например, не сможет подобрать stepwise_size.
Я написал небольшую обертку вокруг этой функции под названием BaseFitter, которая сохраняет историю параметров и делает другие служебные вещи. Но в конце концов всё сводится к вызову minimize.
Основная идея простая. Для промежутка t_vals получаем предсказания заражений в день, смертей в день и выздоровлений в день. Вычисляем отклонения предсказанных значений от реальных и кладем всё это в один массив.
Также применяется несколько трюков, до которых пришлось дойти методом эмпирического тыка.
Во-первых, количество новых зараженных и количество новых смертей имеют абсолютно разный масштаб: нормально видеть 1000 новых зараженных за день и лишь 1 смерть в тот же день. Если ориентироваться на абсолютные остатки, то оптимизация будет “обращать внимание” только на остатки по зараженным. Чтобы привести все остатки к одному масштабу я применил трансформацию к относительной ошибке с помощью функции smape_resid_transform.
Во-вторых, можно предположить, что статистика по смертям достовернее статистики по заражениям и выздоровлениям. Чтобы внести это предположение в оптимизацию вводятся веса (self.weights) для остатков. Хорошо сработали такие веса: 0.5 для остатков по смертям и 0.25 для остальных.
Тренируем модель
Наконец, натренируем SEIRD со скрытыми состояниями. Статистика вносится с некоторым лагом по времени. Чтобы это меньше влияло на нашу модель будем использовать сглаженные версии колонок для расчета остатков.
from sir_models.fitters import HiddenCurveFitter
from sir_models.models import SEIRHidden
stepwize_size = 60
weights = {
'I': 0.25,
'R': 0.25,
'D': 0.5,
}
model = SEIRHidden(stepwise_size=stepwize_size)
fitter = HiddenCurveFitter(
new_deaths_col='deaths_per_day_ma7',
new_cases_col='infected_per_day_ma7',
new_recoveries_col='recovered_per_day_ma7',
weights=weights,
max_iters=1000,
)
fitter.fit(model, train_subset)
result = fitter.result
result
Полученные параметры:
Проверим фит модели на тренировочных данных:
Вот это другое дело! Модель показывает, что почти половина смертей не попадают в статистику. По заражениям другая картина: в статистику попадает примерно одна пятая.
Полезно взглянуть на все предсказываемые моделью компоненты: ежедневные смерти, заражения и выздоровления. Модель может выдавать абсолютно верные предсказания по смертям, но при этом прогнозировать в 10 раз больше выздоровлений, или наоборот.
Отлично, здесь тоже всё выглядит нормально. В некоторых местах модель достаточно сильно ошибается, но нас это устраивает: нам не нужен идеальный фит на тренировочных данных. Модель верно захватывает общий тренд. Значит, она нормально описывает “механизм эпидемии”, даже если ошибается в конкретные дни.
Верифицируем модель c помощью кросс-валидации
Хорошие графики на тренировочных данных это одно, а качество на реальных данных это совсем другое. Хоть мы и не строим прогнозную модель, но единственный способ понять, что она способна описать эпидемию — это проверить качество прогноза.
В статьях по моделированию COVID-19 стандартом является проверять модель на предсказаниях кумулятивного числа погибших, поэтому сделаем так же.
Процесс верификации:
Выбираем несколько дат из тренировочных данных, например каждый 20-ый день.
Для каждой даты:
Обучаем модель на всех данных до этой даты.
Делаем прогноз суммарного количества погибших на 30 дней вперед.
Считаем ошибку предсказания.
Вычисляем среднюю ошибку модели.
Сравниваем ошибку с ошибкой бейзлайна: предсказанием предыдущего дня.
from sir_models.utils import eval_on_select_dates_and_k_days_ahead
from sir_models.utils import smape
from sklearn.metrics import mean_absolute_error
K = 30
last_day = train_subset.date.iloc[-1] - pd.to_timedelta(K, unit='D')
eval_dates = pd.date_range(start='2020-06-01', end=last_day)[::20]
def eval_hidden_moscow(train_df, t, train_t, eval_t):
weights = {
'I': 0.25,
'R': 0.25,
'D': 0.5,
}
model = SEIRHidden()
fitter = HiddenCurveFitter(
new_deaths_col='deaths_per_day_ma7',
new_cases_col='infected_per_day_ma7',
new_recoveries_col='recovered_per_day_ma7',
weights=weights,
max_iters=1000,
save_params_every=500)
fitter.fit(model, train_df)
train_initial_conditions = model.get_initial_conditions(train_df)
train_states, history = model.predict(train_t, train_initial_conditions, history=False)
test_initial_conds = [compartment[-1] for compartment in train_states]
test_states, history = model.predict(eval_t, test_initial_conds, history=False)
return model, fitter, test_states
(models, fitters,
model_predictions,
train_dfs, test_dfs) = eval_on_select_dates_and_k_days_ahead(train_subset,
eval_func=eval_hidden_moscow,
eval_dates=eval_dates,
k=K)
model_pred_D = [pred[7] for pred in model_predictions]
true_D = [tdf.total_dead.values for tdf in test_dfs]
baseline_pred_D = [[tdf.iloc[-1].total_dead]*K for tdf in train_dfs]
overall_errors_model = [mean_absolute_error(true, pred) for true, pred in zip(true_D, model_pred_D)]
overall_errors_baseline = [mean_absolute_error(true, pred) for true, pred in zip(true_D, baseline_pred_D)]
print('Mean overall error baseline', np.mean(overall_errors_baseline).round(3))
print('Mean overall error model', np.mean(overall_errors_model).round(3))
overall_smape_model = [smape(true, pred) for true, pred in zip(true_D, model_pred_D)]
np.median(overall_smape_model)
Результат:
Mean Absolute Arror бейзлайна: 714.
Mean Absolute Arror модели: 550.
Symmetric Mean Absolute Percentage Error: 4.6%
Модель побила бейзлайн и ошибка в пределах 5% Можно заключить, что модель подходит для оценки ситуации с двумя штаммами.
Расширение модели для двух штаммов
Ситуацию с двумя штаммами можно смоделировать как две параллельные эпидемии, которые заражают людей из одной популяции. При этом зараженные одним штаммом не могут заразиться другим. В контексте SEIR моделей это означает, например, что вместо группы I(t) для всех зараженных у нас теперь будет две группы для разных штаммов: I1(t) и I2(t).
Модель эпидемии обычного SARS-CoV-2 мы только что обучили. Осталось получить модель для “британского” штамма. Согласно исследованиям B.1.1.7 отличается только параметром R0: он в 1.4 - 1.9 раз больше. Значит мы можем взять обученную модель для обычного SARS-CoV-2, увеличить R0 и получить модель для B.1.1.7.
Полная схема модели с двумя штаммами выглядит так:
Главное отличие реализации этой модели в коде от предыдущих в том, что эта модель не обучается, а создается на основе обученной модели для одного штамма. Добавляется параметр beta2_mult, который задает, на сколько надо умножить β1(t) первого штамма, чтобы получить β2(t) второго.
Мы предполагаем, что меры карантина и всё остальное действуют на новый штамм так же, как на старый, а так же что уровень карантина в будущем сохраняется такой же, как в последний день тренировочных данных.
Сценарии развития эпидемии при появлении B.1.1.7
Наконец, мы получили модель для двух штаммов. Неизвестно какое именно R0 у B.1.1.7, а так же сколько сейчас в Москве носителей этого штамма. Рассмотрим несколько сценариев.
Значение R0 влияет на дату и высоту пика заражений новым штаммом. В лучшем случае B.1.1.7 просто продлевает эпидемию в текущем состоянии на полгода-год. В худшем случае случается большая волна заражений.
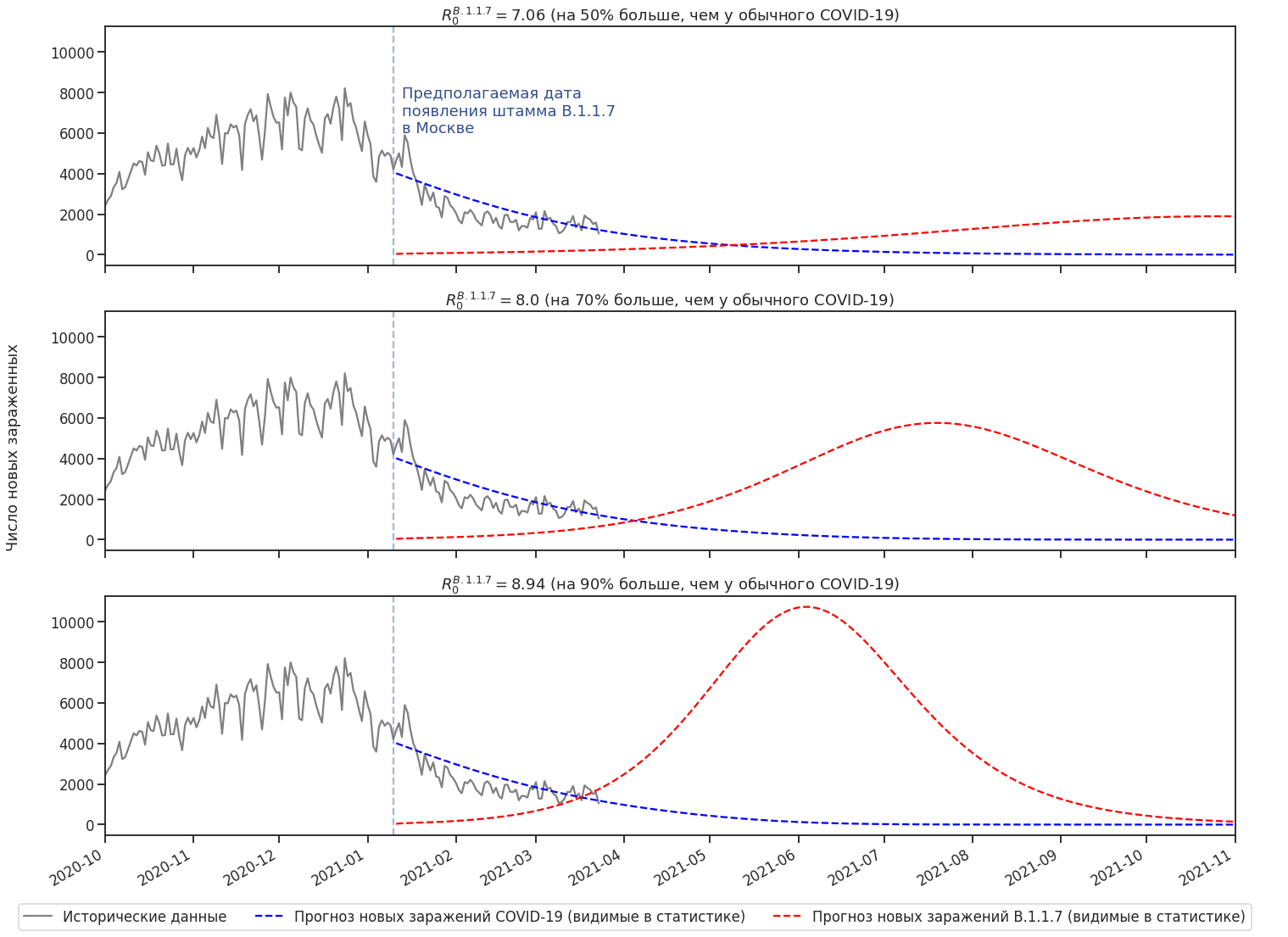
Изначальное количество носителей “британского штамма” влияет только на дату пика. Во всех случаях новая волна случается в течение года после появления нового штамма.
Ослабление карантина приводит к значительному количеству заражений.
