https://habr.com/en/company/bitfury/blog/440274/- Bitfury Group corporate blog
- Development for e-commerce
- Distributed systems
- Finance in IT
Zero-knowledge proofs/arguments are an emerging cryptographic technology that promises to bring us closer to the Holy Grail of blockchain: providing data privacy and auditability.
Potential applications for zero-knowledge include, but are not limited to:
Another application for zero-knowledge proofs is helping blockchains
scale. ZKPs allow for the “compressing” of computations for blockchain transactions without sacrificing security.
In this article, we describe how zero-knowledge (specifically, Bulletproofs) can be applied to build a privacy-focused service using Bitfury’s Exonum platform.

Situational Analysis
It is possible to achieve
some level of data privacy in blockchain apps using the “walled garden” approach, where the data is hidden because access to it is restricted with the help of firewalls, role-based access control,
moats and other perimeter security measures. Sensitive data in the blockchain may be encrypted (perhaps, with a public-key encryption scheme, with the relevant public keys managed by the same blockchain) and/or stored outside of the blockchain (in this case, the blockchain stores only hash fingerprints of the data). This approach is used in many permissioned distributed ledger frameworks.
However, the disadvantages of the “walled garden” approach are becoming increasingly apparent. To put it bluntly, the approach is antithetical to one of the main selling points of blockchain — auditability. If the data on the blockchain cannot be audited by consulting smart contract logic, the blockchain becomes a glorified
linked timestamping service. The fact that there is some data on the blockchain no longer means that this data is valid as per smart contract rules. The second major disadvantage to the walled garden approach is that it does not scale. R3’s CTO Richard Brown, for example, aptly
compared the privacy model of their solution to Slack channels — it is difficult to securely add or remove participants from the garden, even more so when there are no prior expectations as to the number and identities of these participants.
This is where
zero-knowledge can be valuable. By design, zero-knowledge proofs and arguments¹ convincingly prove a statement about private data without revealing anything about the data except the statement being proved. It is easy to make zero-knowledge proofs
universally verifiable, without sacrificing any privacy!² This feature is exactly what is needed to build a system that is both privacy-preserving and auditable at the same time.
Our Research
To demonstrate the use of zero-knowledge proofs, we are going to build a cryptocurrency service with similar functionality to the tutorial services in the
Exonum documentation. The service makes it possible to register users and wallets (providing an initial token balance as a reward) and transfer tokens among registered parties. All transactions are authenticated with the help of a digital signature cryptosystem, Ed25519, which is built into Exonum services. We do not hide identities of transacting parties (i.e., their public keys), but we hide the number of tokens being transacted and the balance of each account in the system. We also discuss how we could improve the service to hide the transacting entities at the end of the article.
The service is fully open-sourced and can be accessed
here.
Cryptography Background
In order to understand how the service works, we first need to introduce ourselves to the core cryptographic primitive underpinning Bulletproofs — a concept called
Pedersen commitments. A cryptographic commitment scheme is somewhat like a hash function: someone inputs secret data (the opening) and gets the output that is unrecognizably scrambled (the commitment). One can then reveal the opening to prove that the committed value corresponds to it.
The difference with hash functions is that besides being
binding (no one can devise two different openings producing the same commitment), a commitment scheme is also expected to be
hiding (it is impossible to reverse the scheme and produce an opening given a commitment). A hash function is hiding if its input is uniformly distributed about the entire input space, but this assumption most frequently does not hold for commitments (indeed, it must be possible to commit to a value from a very small set, such as Boolean). As such, the opening contains, besides the payload, the
blinding factor which makes it (at least statistically) improbable to guess the payload given the commitment.
The Pedersen commitment scheme uses a
prime-order group, in which the
discrete logarithm problem (DLP) is believed to be hard, together with two generators,
G and
H.
G and
H must be chosen in such a way that the discrete log relation among them is unknown; in other words, no one knows
k such that
H = kG.³ The opening is a pair
(x,r), where
x is the committed value and
r is the blinding factor; both are group scalars (essentially, integers with “overflow” akin to finite integer types used in most programming languages). The commitment is computed as
Comm(x;r) = xG + rH. It can be proven that if DLP in the group is hard, the Pedersen commitment is computationally binding and perfectly hiding.⁴
The crucial property for Pedersen commitments is that they are additive: the sum (or difference) of 2 commitments is a commitment to the sum (or difference) of committed values. Indeed,
C1 = x1 G + r1 H; C2 = x2 G + r2 H =>
C1 + C2 = (x1 + x2) G + (r1 + r2) H = Comm(x1 + x2; r1 + r2).
We do not include the details here on how bulletproofs are built and verified, but more information can be found in the following resources — [
1] and [
2]. It suffices to note that the upper range bound
M is assumed to have form
2^(2^n), which leads to the most efficient proof construction.
Building a Service
With our knowledge, we can securely hide account balances and transfer amounts with the help of Pedersen commitments. Using range proofs, we can prove / verify that a transfer is correct:
- The transferred amount is positive
- The sender has enough balance in his/her account.
For the first proof, we take the commitment to the transfer amount,
C_a (it is directly present in the transfer transaction), and verify that the value committed in
C_a-Comm(1;0) lies in the range
[0,M). Indeed, this is equivalent to proving that
C_a corresponds to a value in the range
[1,M]. The sender can produce this proof, as s/he knows the transferred amount
a.
For the second proof, we need to take the commitment for the sender’s current balance,
C_s, and verify that the value committed in
C_s-C_a lies in the range
[0,M). Again, the sender can produce this proof as s/he knows the opening to both
C_s and
C_a.
To apply the transfer to the blockchain state, we subtract amount commitment
C_a from the sender’s balance commitment (as we have verified, it cannot lead to a negative balance, or to the increase of the sender’s balance), and then add
C_a to the receiver’s balance commitment.
Key Details
It is important to note that there are a few conditions that can make the implemented service more complex.
The receiver of a transfer must find out the opening to
C_a from somewhere; otherwise, s/he ceases to know the opening to his/her balance and can no longer do anything with his/her wallet. The opening is not present in the plaintext of the transfer transaction (which is the entire point). We
could assume that the receiver reliably obtains the opening via an off-chain channel (for example, sent by the sender via Telegram), but that is not an illustrative scenario. So instead, we encrypt the opening using two-party public-key encryption based on Diffie-Hellman key exchange (libsodium calls this type of encryption
box). For the added benefit, Curve25519 keys required for the
box routine can be converted from Ed25519 keys, so we may continue to use a single keypair for each user instead of introducing separate encryption keys.⁵

Once we introduce encryption, we can no longer apply the transfer atomically. Indeed, the sender can maliciously or unintentionally provide garbage instead of the opening encryption, and the blockchain logic won’t be able to tell that this is the case.⁶ Thus, we request the receiver to explicitly accept the transfer via a separate transaction.
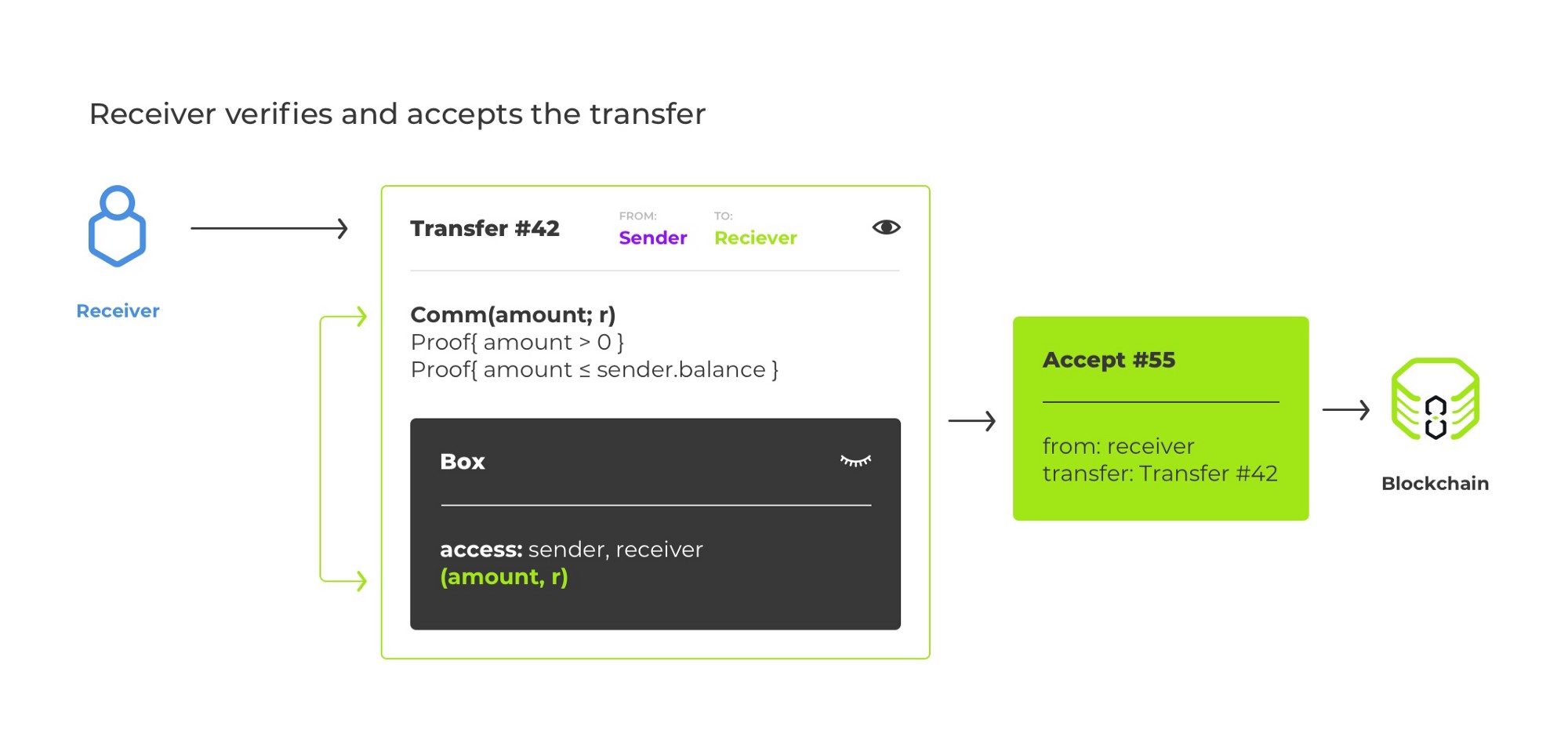
Before a transfer is accepted, it modifies the sender’s balance commitment (otherwise, we would allow double-spending!), but not the receiver’s one.

Once the acceptance transaction is confirmed by the blockchain network, the receiver’s balance is updated, and the transfer is complete.

To prevent deadlocks, a transfer specifies a time-lock delay (in relative blockchain height,
a la Bitcoin’s
CSV) for the receiver to signal acceptance. If the time lock is expired, the transfer is automatically refunded to the sender (Exonum allows this via
Service::beforeCommit() hook).
Another issue is more intricate. In order to produce the proof of a sufficient balance, the sender needs to know his/her current balance, which may not always be the case. A stray acceptance transaction or refund may increase the sender’s balance unwittingly to him/her; in this case, the transfer will fail verification, and the sender will be reasonably frustrated.
To alleviate this problem, we allow transfers to reference what the sender thinks is his/her current wallet state (more precisely, the reference takes form of the number of events changing account balance — transfers and refunds). When checking the proof of a sufficient balance, we use the referenced state to obtain the sender’s balance commitment. Additionally, we check that no outgoing transfers have occurred since the referenced state. If this is the case, we can be certain that if we subtract the transfer amount from the sender’s
current balance, we will end up with a non-negative value. Indeed, the events in the account history after the reference point (incoming transfers and refunds) can only increase the balance!⁷
With reference points in place, the sender is still somewhat constrained; s/he must have no pending transfers when creating a new transfer. Still, this restriction is much less limiting than the requirement to know one’s account state at the moment of the transfer; fundamentally, we make the sender dependent on what
s/he did previously, but not on others’ actions.
Implementation
We use a bulletproofs library written in pure
Rust, which has recently reached
pre-release stage. Since the Exonum platform is written in Rust, it integrates with the library seamlessly. As a bonus, unlike the version of bulletproofs described in the original whitepaper (which is being developed in
C and uses Bitcoin’s secp256k1 elliptic curve), the library we use is based upon Curve25519, which is already used in Exonum as the main component of the Ed25519 digital signature cryptosystem.
Implementing the service based on the above description is quite straightforward. The most difficult part was constructing Merkle proofs that authenticate information returned to the user so that s/he does not have to blindly trust the Exonum nodes s/he communicates with. Improving experience of service developers in this regard is one of the major goals of the
Exonum 1.0 release.
Next Steps
The service we have built does not hide the identities of the sender and the receiver of transfers, which is a major limitation for real-world applications. Fortunately, there are ways to solve this problem.
The generic technique used in
zCash (but principally applicable to other use cases, such as
Ethereum) is based on creating a
Merkle tree of the system state. For example, zCash builds the
note commitment tree, which is roughly equivalent to ever created transaction outputs in Bitcoin. Zero-knowledge proofs then encompass authentication paths (aka Merkle branches) in this tree, reveals something about an element of the tree without revealing which element is referred to. The downside of this approach is that cryptographic hash functions used to build Merkle trees are difficult to transfer into the zero-knowledge realm; the resulting proofs become computationally expensive — a single proof can take seconds or even minutes to create. Searching for more “ZKP-friendly” cryptographic hash functions is the area of active research.
If we admit additional constraints, there may be an easier solution. For example, a recent paper by
Narula et al. describes a system with a limited, a priori known number of participants, which can transact among themselves without revealing participants or transferred amounts for any transaction. (Think a privacy-focused blockchain network for inter-bank transfers.)
On a more prosaic note, there are probably many technical improvements that the developed service can enjoy: more test coverage, separation of signing and encryption keys, benchmarking, etc. A major improvement to the service UX would be enabling deterministic ordering of transactions originating from the same user, which we plan to solve not long after releasing Exonum 1.0.
Conclusion
We have described how to construct an account-based cryptotoken with strong privacy enabled by zero-knowledge proofs (specifically, bulletproofs). The token logic was implemented as an Exonum service. Although currently the service is just a proof of concept, it showcases how the Exonum platform can be used to build atop complex cryptographic primitives with very low overhead imposed by the execution environment.
- There is an intricate distinction between proofs and arguments, which we will not get into here. For the sake of simplicity, we will refer to all zero-knowledge constructions in this article as zero-knowledge proofs even if this is not always correct from the theoretical standpoint.
- This can be accomplished via a very general technique known as Fiat — Shamir transform, which converts an interactive proof protocol into a non-interactive, universally verifiable one. Sacrificing scientific rigor once again, we will not explicitly clarify that zero-knowledge proofs we use are non-interactive.
- Generators are usually chosen with a “nothing up my sleeve” method. For example, G may be a part of the group specification for its use in public-key cryptography, and H is derived from G via a hash function: H ~ hash(G).
- The latter means that even an adversary with infinite computing power cannot deduce what the commitment commits to; indeed, if DLP in the group is broken, every commitment can be opened to any possible value.
- This is partially a proof-of-concept decision; in general, reusing keys for different purposes is a bad idea.
- It is theoretically possible to provide a zero-knowledge proof for the encrypted value being equivalent to the committed balance; however, it would prohibitively increase the system complexity.
- It bears mentioning that some transfers breaking the “no outgoing transfers since the referenced state” rule can still be correct; we just have no way to verify this.




