https://habrahabr.ru/post/348974/- Разработка под Windows Phone
- Математика
- Алгоритмы
- Python
Введение
В настоящее время в качестве бронебойных боеприпасов широкое применение получили бронебойные оперенные подкалиберные снаряды (БОПС), обладающие высокой проникающей способностью.
Это достигается за счет высокой начальной скорости боеприпаса (1650 – 1840 м/с) и малого поперечного сечения (d = 20-30 мм). Для компенсации силы сопротивления воздуха применяют придание боеприпасу реактивной тяги.
Прямоточный воздушно-реактивный двигатель (ПВРД), прост по конструкции, имеет высокий коэффициент полезного действия при больших числах Маха компактен, поскольку не требует наличие окислителя в составе топлива, так как использует кислород окружающей среды [1].
Принцип работы ПВРД
Воздух со скоростью полёта 30-60 м/с поступает во входное устройство двигателя затормаживается до 0,1-0,2 Маха, при этом кинетическая энергия воздуха преобразуется во внутреннею энергию повышается его давление и температура. Воздух можно считать идеальным газом, поэтому отношение его статического давления к атмосферному определяется соотношением:

(1)
где p – давление в полностью заторможенном потоке; po – атмосферное давление; Mn – число Маха; k– Показатель адиабаты равный 1,4.
Сжатый воздух попадая из входного устройства в камеру сгорания нагревается за счёт окисления подаваемого в неё топлива. Образующаяся из смеси воздуха с продуктами горения газовая смесь – рабочее тело в сопле достигает звуковой скорости, а на его выходе расширяясь до сверхзвуковой.
Рабочее тело вытекает со скоростью большей скорости встречного потока воздуха что и создаёт реактивную тягу.
Когда скорость полёта значительно меньше скорости реактивной струи, тяга растёт. С приближением скорости полёта к скорости реактивной струи тяга падает, проходя некий максимум, соответствующий оптимальной скорости полёта. Схемы работы прямоточного реактивного двигателя на жидком и твёрдом топливе приведены соответственно на рисунках 1,2:


Сила тяги ПВРД определяется из соотношения:

(2)
где: P– сила тяги; v– скорость полёта; ve – скорость реактивной струи относительно двигателя; dmf/dt – секундный расход топлива.
Секундный расход воздуха определяется по формуле:

(3)
где

– плотность воздуха (зависит от высоты); dV/dt– объём воздуха, который поступает в воздухозаборник ПВРД в единицу времени; S – площадь сечения входа воздухозаборника; v – скорость полёта.
Чтобы определить секундный расход рабочего тела для идеального случая, когда горючее полностью сгорает и полностью используется кислород воздуха в процессе горения, воспользуемся формулой:
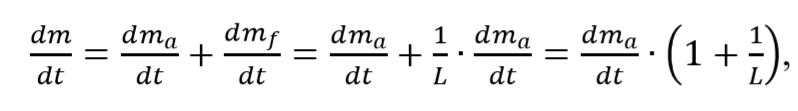
(4)
где: L – стехиометрический коэффициент горючего и воздуха.
С развитием технологии смесевого твёрдого топлива оно стало применяться в ПВРД. Топливная шашка с продольным центральным каналом размещается в камере сгорания. Рабочее тело проходя по камере сгорания окисляет топливо с его поверхности и нагревается само.
Использование твёрдого топлива ещё больше упрощает конструкцию ПВРД поскольку становиться не нужной камера сгорания.
Основную часть наполнителя смесевого топлива ПВРД составляет мелкодисперсный порошок алюминия, магния или бериллия теплота сгорания, которых значительно превосходит теплоту сгорания углеводородных горючих.
Примером твердотопливного ПВРД может служить маршевый двигатель противокорабельной ракеты П-270 Москит.
В зависимости от скорости полёта ПВРД разделяются на дозвуковые, сверхзвуковые и гиперзвуковые. Это разделение обусловлено конструктивными особенностями каждой из этих групп.
В сверхзвуковом диапазоне ПВРД значительно более эффективен чем в дозвуковом. Например, при скорости М=3 степень повышения давления у ПВРД составляет 37, что сравнимо с самыми высоконапорными компрессорами турбореактивных двигателей.
Конструкция БОПС с ПВРД
Одним из главных параметров, который позволяет оценить конструкцию снаряда — это низкая сила сопротивления воздуха. Рассмотрим один из известных бронебойных оперенных подкалиберных снарядов БМ-9 с твёрдотопливным двигателем.
Конструкция БМ-9 и результаты её аэродинамических исследований в программе Solidworks, полученные в работе [2], приведены на следующих рисунках 3,4,5. Конечна скорость БМ-9 составляет 1500 м/с в момент прибытия на расстоянии 2120 м.

Рисунок 3. – Бронебойный подкалиберный снаряд БМ-9

Рисунок 4 –Распределение давления воздушного потока, создаваемое при полёте БМ-9.

Рисунок 5 –Распределение скоростей воздушного потока, создаваемое при полёте БМ-9
Расчет силы сопротивления воздуха при движении БОПС
Для построения закона силы сопротивления воздуха, требуется обработать экспериментальные данные полученные в работе [2] (см. таблицу) для формы снаряда (рис.3) и выразить зависимость между скоростью и силой сопротивления воздуха.

Привожу листинг программы на Python, который демонстрирует возможности решения задачи получения функции Rc(V) в удобном для дальнейшего использования виде:
Графики функции силы сопротивления воздуха от скорости# -*- coding: utf8 -*-
import numpy as np
from scipy.integrate import odeint
import scipy as sp
from scipy.interpolate import interp1d
import matplotlib.pyplot as plt
x =np.array([1800, 1700, 1600,1500,1400 ,1300 ,1200, 1100])
y =np.array([ 1102, 979, 836, 705, 603, 534, 2717,2029])
new_length = 800
new_x = np.linspace(x.min(), x.max(), new_length)
new_y = sp.interpolate.interp1d(x, y, kind='cubic')(new_x)
plt.figure()
plt.title('График Rc(V) с интерполяцией прямыми линиями')
plt.ylabel('Сила сопротивления воздуха Rc(V) в н')
plt.xlabel('Скорость перемещения в воздухе V в м/с')
plt .plot(x,y,'r',linewidth=2,label='Закон изменения сопротивления от скорости')
plt .plot(x,y,'o',label='Экспериментальные данные')
plt.legend(loc='best')
plt.grid(True)
plt.figure()
plt.title('График Rc(V) с интерполяцией кубическим сплайном')
plt.ylabel('Сила сопротивления воздуха Rc(V) в н')
plt.xlabel('Скорость перемещения в воздухе V в м/с')
plt .plot(new_x,new_y,'r',linewidth=2,label='Закон изменения сопротивления от скорости')
plt .plot(x,y,'o',label='Экспериментальные данные')
plt.legend(loc='best')
plt.grid(True)
plt.figure()
plt.title('График Rc(V)')
plt.ylabel('Сила сопротивления воздуха Rc(V) в н')
plt.xlabel('Скорость перемещения в воздухе V в м/с')
plt .plot(new_x,new_y,'r',linewidth=2,label='Закон изменения сопротивления от скорости')
plt .plot(x,y,'o',label='Экспериментальные данные')
w_x=1800
w_y = sp.interpolate.interp1d(x, y, kind='cubic')(w_x)
plt .plot(w_x,w_y ,'o',label='Значение функции Rc(%s) -%s'%(w_x,w_y))
plt.legend(loc='best')
plt.grid(True)
plt.figure()
x =np.array([1800, 1700, 1600,1500,1400 ,1300])
y =np.array([ 1102, 979, 836, 705, 603, 534])
new_length = 400
new_x = np.linspace(x.min(), x.max(), new_length)
new_y = sp.interpolate.interp1d(x, y, kind='cubic')(new_x)
plt.title('Рабочий график Rc(V)')
plt.ylabel('Сила сопротивления воздуха Rc(V) в н')
plt.xlabel('Скорость перемещения в воздухе V в м/с')
plt .plot(new_x,new_y,'r',linewidth=2,label='Закон изменения сопротивления от скорости')
plt .plot(x,y,'o',label='Экспериментальные данные для 1800 ..1300 м/с')
plt.legend(loc='best')
plt.grid(True)
plt.show()
Получим:



Данный график нам показывает, что если при вылете из ствола скорость снаряда в идеальном случае, достигает 1800 м/с, то этой скорости соответствует значение силы сопротивления воздуха 1102 Н.
При снижении скорости на траектории сила сопротивления падает по закону, который изображён на графике. Далее при скорости примерно 1200 м/с сила сопротивления начинает расти. Такое явление связано с геометрией конфузора на входе воздухозаборника ПВРД.
На реактивных самолётах для борьбы с указанным явлением применяют регулируемый конус воздухозаборника. Для рассматриваемого снаряда это невозможно из-за более высоких скоростей полёта в пределах (1300...1800) м/c. Поэтому диапазон экспериментальных данных нужно ограничить для получения рабочего графика:

Функцию Rc(v) для любого набора экспериментальных можно получить из следующего короткого листинга:
# -*- coding: utf8 -*-
import numpy as np
import scipy as sp
from scipy.interpolate import interp1d
x =np.array([1800, 1700, 1600,1500,1400 ,1300 ,1200, 1100])
y =np.array([ 1102, 979, 836, 705, 603, 534, 2717,2029])
def Rc(new_x):
new_y = sp.interpolate.interp1d(x, y, kind='cubic')(new_x)
return new_y
Расчет внешней баллистики БОПС
Поскольку выстрел с прицеливание производится из определённого ствола нас будет интересовать дальность с учётом силы тяги.
Определение силы тяги
Пользуясь всеми формулами (2)÷(4) можно определить силу тяги. Для начала определим секундный расход воздуха:

где

=1.205 кг/м3 (Плотность воздуха из уравнения Клапейрона при T=0℃); V=1800 м /с − скорость движения снаряда (по условию).
Площадь сечения входа воздухозаборника:

Секундный расход горючего, которое будет соответствовать секундному расходу воздуха:

где L = 14,7; что соответствует реактивному топливу «РТ» (таблица)
Таблица − Стехиометрический состав горючей смеси, выраженный как отношение окислителя к горючему.

По данным [2] скорость реактивной струи для приведенных параметров равна V=1840 м/с. Определяем силу тяги из соотношения (2):

Система уравнений внешней баллистики
Рассмотрим схему сил действующих на центр масс неуправляемого в полёте снаряда:

Система уравнений проймёт вид:

(5)
Численные значения параметров:

(6)
Начальные условия:

(7)
Систему дифференциальных уравнений (5) с учётом (6) и (7) будем решать средствами Python, переопределив переменные как y1,y2,y3,y4:
Численное решение системы дифференциальных уравнений# -*- coding: utf8 -*-
import numpy as np
from scipy.integrate import odeint
import scipy as sp
from scipy.interpolate import interp1d
import matplotlib.pyplot as plt
#Экстраполяция данных в точку 1900 м/c
x =np.array([1900,1800, 1700, 1600,1500,1400 ,1300])
y =np.array([ 1225,1102, 979, 836, 705, 603, 534])
def Rc(new_x): # Кубический сплайн
new_y = sp.interpolate.interp1d(x, y, kind='cubic')(new_x)
return new_y
def f(y,t):#Запись дифференциальных уравнений системы внешней баллистики
y1,y2,y3,y4=y
return [-9.81*np.cos(y1)/y2, 1181/6.77 -Rc(y2)/6.77 -9.81*np.sin(y1),y2*np.cos(y1),y2*np.sin(y1)]
t=np.linspace(0,1.2,50)# Массив времён
y0=[0.18*np.pi/180,1800,0,0]#Начальные условия - угол, скорость, перемещение высота
[y1,y2,y3,y4]=odeint(f,y0,t,full_output=False).T# Решение системы в виде списков
plt.figure()
plt.title('График траектории по времени')
plt.ylabel('Высота в м')
plt.xlabel('Время в с')
plt .plot(t,y4,'r',linewidth=2,label='Время -%s с.'%max(t))
plt.legend(loc='best')
plt.grid(True)
plt.figure()
plt.title('График распределения скорости по траектории')
plt.ylabel('Скорость в м/c')
plt.xlabel('Перемещение снаряда в м')
plt .plot(y3,y2,'b',linewidth=2,label='Перемещение снаряда-%s м.'%round(max(y3),1))
plt.legend(loc='best')
plt.grid(True)
plt.figure()
plt.title('График распределения скорости по времени')
plt.ylabel('Скорость в м/c')
plt.xlabel('Время в с')
plt .plot(t,y2,'g',linewidth=2,label='Ударная скорость снаряда -%s м/с'%round(max(y2),1))
plt.legend(loc='best')
plt.grid(True)
plt.figure()
plt.title('График траектории')
plt.ylabel('Высота в м')
plt.xlabel('Перемещение в м')
plt .plot(y3,y4,'m',linewidth=2,label='Максимальная высота -%s м. '%round(max(y4),1))
plt.legend(loc='best')
plt.grid(True)
plt.show()
Получим:



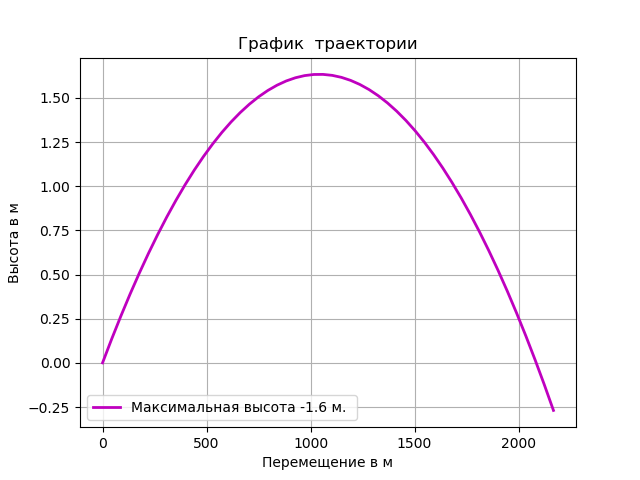
Баллистические характеристики приведены на графиках, отрицательные области сохранены для наглядности перехода через ноль.
Выводы
Рассмотрены особенности бронебойных снарядов с прямоточным воздушно- реактивным двигателем, основные расчёты выполнены с применение средств высокоуровневого языка программирования Python.
Ссылки:
1. Артёмов О.А. Прямоточные воздушно-реактивные двигатели (расчет характеристик): Монография. — М: Компания Спутник+, 2006. — 374 с.
2.
Гаврилов К.С. Проектирование бронебойного подкалиберного снаряда с прямоточным воздушно-реактивным двигателем. 
 (1)
(1)

 (2)
(2) (3)
(3) – плотность воздуха (зависит от высоты); dV/dt– объём воздуха, который поступает в воздухозаборник ПВРД в единицу времени; S – площадь сечения входа воздухозаборника; v – скорость полёта.
– плотность воздуха (зависит от высоты); dV/dt– объём воздуха, который поступает в воздухозаборник ПВРД в единицу времени; S – площадь сечения входа воздухозаборника; v – скорость полёта.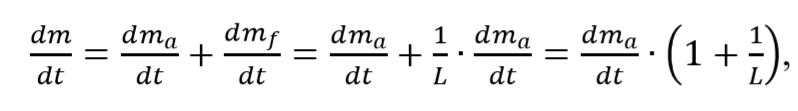 (4)
(4)








 =1.205 кг/м3 (Плотность воздуха из уравнения Клапейрона при T=0℃); V=1800 м /с − скорость движения снаряда (по условию).
=1.205 кг/м3 (Плотность воздуха из уравнения Клапейрона при T=0℃); V=1800 м /с − скорость движения снаряда (по условию).




 (5)
(5) (6)
(6) (7)
(7)


