news.shamcode.ru | Более быстрые хеш-таблицы: претенденты на место SwissTable

24 ноября 2021 года на сайте ArXiv.org была опубликована научная статья «Крошечные указатели» (Tiny Pointers) с описанием новой структуры данных — «крошечных» указателей, которые указывают путь к фрагменту хранимых данных и занимают меньше памяти, чем традиционные указатели.

Осенью 2021 года эту статью заметил Андрей Крапивин (Andrew Krapivin), студент Ратгерского университета в Нью-Джерси, и не придал ей особого значения, пишет Quanta Magazine, журнал о последних достижениях в математике (перевод статьи на Хабре). Только через два года он нашёл время, чтобы внимательно ознакомиться с материалом. И понял, насколько это прорывное изобретение, если применить его для оптимизации хеш-таблиц.

Данная тема уже упоминалась на Хабре, но заслуживает более подробного обсуждения.

Хеш-таблицы

Хеш-таблица — структура данных, реализующая интерфейс ассоциативного массива. Она позволяет хранить пары (ключ, значение) и выполнять три операции:

добавления новой пары;
поиска пары по ключу;
удаления.

… или

INSERT(ключ, значение)
FIND(ключ)
REMOVE(ключ)

Предполагается, что ассоциативный массив не может хранить две пары с одинаковыми ключами.

Важное свойство хеш-таблиц состоит в том, что, при некоторых разумных допущениях, все три операции (добавление, удаление, поиск) в среднем выполняются за время $inline$ .

Важной частью хеш-таблиц является проверка на совпадения значений (коллизии). Существует несколько способов разрешения коллизий: метод списков (2-choice hashing) и открытая адресация. Во втором случае в массиве хранятся сами пары ключ-значение.

И при поиске коллизий, и при обычных операциях требуется проверять ячейки в некотором порядке — эта операция называется пробирование. Например, если ячейки проверяются по порядку, то это называется линейным пробированием.

Пример хеш-таблицы с открытой адресацией и линейным пробированием, получающейся при вставке элементов в левой колонке сверху вниз

Хеш-таблицы получили широкое распространение в программировании отчасти благодаря своей простоте и удобству использования. Они эффективно и очень просто выполняют три операции, названные выше. Первые хеш-таблицы появились ещё в начале 1950-х годов. С тех пор специалисты изучают и используют их. Среди прочего, им была интересна предельная скорость выполнения некоторых операций. Например, насколько быстрым может быть поиск или вставка?

Ответ зависит от времени, которое требуется для поиска пустого места в хеш-таблице. Это, в свою очередь, зависит от того, насколько она заполнена. Заполненность можно описать в процентах: 50% или 90%, но часто мы имеем дело с гораздо более полными таблицами, поэтому вместо процентов используется целое число $inline$ . Это коэффициент загрузки, который указывает на расстояние от стопроцентного заполнения. Если $inline$ , то таблица заполнена на 99%. Если $inline$ , то таблица заполнена на 99,9% и т. д. Этот показатель даёт возможность оценить время поиска или вставки. При линейном пробировании максимальное время поиска или вставки равно $inline$ . Например, если хеш-таблица заполнена на 99%, то нужно просмотреть максимум 100 позиций, чтобы найти свободное место. Если она заполнена на 99,9%, то 1000 позиций и т. д.

Крошечные указатели

Статья 2021 года представила новый объект структуры данных — крошечные указатели, которые позволяют во многих приложениях заменить традиционные указатели размером $\log {n}$ на $Θ(\log {n})$ — крошечные указатели с очень маленьким оверхедом по времени.

Авторы разработали всеобъемлющую теорию крошечных указателей и привели для них оптимальные конструкции фиксированного и переменного размера. Если крошечный указатель ссылается на элемент массива с коэффициентом загрузки $inline$ , то оптимальный размер фиксированного указателя составляет $Θ(\log \log \log n+\log k)$ бит, а переменного — $Θ(\log k)$ в случае переменного размера. Авторы пишут, что введение крошечных указателей потребовало пересмотра пяти классических задач в науке о данных, в том числе:

В любом двоичном дереве можно выполнять запросы с постоянными затратами времени, и его можно даже сделать в пределах $inline$ бит от оптимального, если допустить модифицикации по времени $Θ(\log^*n)$ . И это справедливо даже для деревьев с поворотом, таких как расширяющееся дерево и красно-чёрное дерево.

Теория позволяет уменьшить объём памяти, занимаемый указателями.

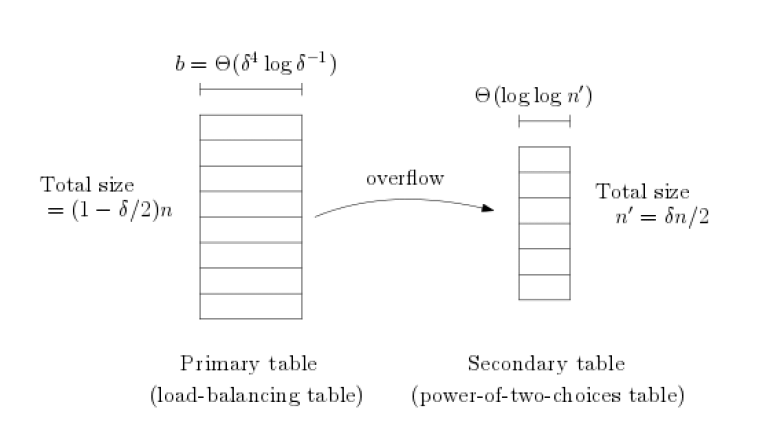
В частности, для указателей фиксированного размера они предложили использовать вторую вспомогательную таблицу для балансировки нагрузки. Она поддерживает гораздо более разреженную загрузку и может успешно хранить все сверхлимитные элементы из основной таблицы в процессе вставки:

Для указателей переменного размера предлагается следующая архитектура:

Один из авторов статьи — Мартин Фарах-Колтон (Martín Farach-Colton), бывший профессор Ратгерского университета и преподаватель Крапивина. Возможно, по этой причине Андрей и заметил данную статью сразу после публикации. Наверное, профессор выдал её студентам для изучения.

Новый алгоритм

Прочитав статью про крошечные указатели, Крапивин вскоре придумал, как ещё больше миниатюризировать указатели, чтобы они занимали меньше памяти. Для этого ему понадобился лучший способ организации данных, на которые указывают указатели.

Андрей Крапивин

В процессе он понял, что изобрёл новый вид хеш-таблицы, которая работает быстрее, чем ожидалось: на поиск определённых элементов уходит меньше времени и шагов.

В статье 1985 года учёный Эндрю Яо (Andrew Yao), который впоследствии получил премию Тьюринга, выдвинул гипотезу, что оптимальный способ найти отдельный элемент или свободное место в хеш-таблице — это перебор в случайном порядке, то есть равномерное зондирование (uniform probing).

В течение 40 лет большинство учёных считали, что гипотеза Яо верна.

Но Андрей Крапивин просто не знал об этом научном консенсусе. Таким образом, его исследования с крошечными указателями привели к созданию нового типа хеш-таблицы, которая не зависит от равномерного зондирования. И для неё максимальное время для поиска и вставки пропорционально $(\log x)^2$ , что намного быстрее, чем $inline$ . Этот результат прямо противоречит гипотезе Яо.

Крапивин показал, что даже без переупорядочивания элементов во времени можно построить хеш-таблицу с открытой адресацией, которая достигает гораздо лучших показателей по сложности поиска, чем считалось ранее. Новый алгоритм позволяет находить элементы быстрее, чем с помощью случайного перебора, даже если таблица почти полностью заполнена. Он не только делает поиск быстрее, но и выполняет запросы за постоянное время, независимо от того, насколько таблица заполнена.

Профессор Мартин Фарах-Колтон (на фото справа), соавтор вышеупомянутой научной статьи, сначала скептически отнёсся к новому дизайну хеш-таблиц. Всё-таки это старая и устоявшаяся структура данных, одна из самых изученных в науке о данных. Ускорение операций с хеш-таблицами казалось слишком невероятным, чтобы быть правдой. Он попросил соавтора «Крошечных указателей» Уильяма Кузмала (William Kuszmaul) из Университета Карнеги-Меллон проверить изобретение. Тот отреагировал с восторгом: «Вы не просто придумали эффективные хеш-таблицы, — сказал он студенту. — Вы фактически полностью решили проблему 40-летней давности!»

Сейчас Крапивин учится на старших курсах Кембриджа, вместе с двумя упомянутыми авторитетными учёными 4 января 2025 года он опубликовал работу «Оптимальные границы для открытой адресации без переупорядочивания» (Optimal Bounds for Open Addressing Without Reordering) на сайте ArXiv.org. В статье доказано, что $(\log x)^2$ — это оптимальное непобедимое ограничение для того класса хеш-таблиц, о котором писал Яо.

Помимо опровержения гипотезы Яо, новая статья содержит ещё более удивительный результат. Он относится к смежной, хотя и несколько иной ситуации: в 1985 году Яо рассматривал не только максимальное время выполнения запросов, но и среднее время. Он доказал, что «жадные» хеш-таблицы, в которых новые элементы помещаются в первое попавшееся доступное место, никогда не покажут среднее время лучше $\log x$ .

Крапивин c соавторами решили проверить, применимо ли это ограничение к нежадным хеш-таблицам. И доказали обратное. Они представили нежадную хеш-таблицу со средним временем запроса намного лучше $\log x$ . Фактически, оно вообще не зависит от $inline$ . Как мы уже упомянули выше, это просто константа, которая не зависит от того, насколько заполнена хеш-таблица.

Тот факт, что можно добиться постоянного среднего времени выполнения запроса независимо от заполненности хеш-таблицы, стал совершенно неожиданным даже для самих авторов.

В оригинальной статье подробно описан новый алгоритм. Если опустить математические детали (см. текст в pdf), то впервые для хеш-таблиц постулируются сразу несколько гарантий:

гарантия вставки за ограниченное число операций;
гарантия поиска за ограниченное число операций;
гарантия неподвижности элемента (пока не превысится процент заполнения);
гарантия достижения целевого процента заполнения.

Отзывы

«Это важная работа, — признал известный специалист Алекс Конвей (Alex Conway) из Корнельского технологического института. — Хеш-таблицы — одна из старейших структур данных, которые у нас есть. И они по-прежнему остаются одним из самых эффективных способов хранения данных». По его словам, в этой области до сих пор остаётся несколько нерешённых вопросов, и новая работа «удивительным образом отвечает на несколько из них».

«Этот результат прекрасен тем, что в нём рассматривается и решается такая классическая проблема, — сказал Гай Блеллох (Guy Blelloch) из университета Карнеги-Меллон.

«Они не просто опровергли гипотезу Яо, но и нашли наилучший возможный ответ на этот вопрос, — говорит Сепехр Ассади (Sepehr Assadi) из Университета Ватерлоо — Могло пройти ещё 40 лет, прежде чем мы бы узнали правильный ответ».

Не факт, что результаты это работы немедленно найдут применение в программировании, но это не главное. Важно, что теперь исследователи стали лучше понимать подобные структуры данных. И вполне возможно, что эта работа позволит в будущем создать в реальных системах хранения структуры данных с более высокой производительностью.

История также наталкивает на мысль, что иногда для решения проблемы лучше не знать об ограничениях и трудностях, с которыми сталкивались предшественники. Тем более если те признали проблему нерешаемой. Это уже не первый случай, когда недостаточно опытный исследователь умудряется сделать открытие, о «невозможности» которого просто не знал. Конечно, зачастую он «изобретает велосипед», но иногда случаются и открытия.

Хабрапользователь Роман Левентов leventov (автор нескольких вариантов хеш-таблиц: Koloboke, SmoothieMap, memory-mapped вариации) в своей заметке на Хабре пояснил, что тема оптимизации хеш-таблиц была фактически закрыта после выхода гугловской SwissTable в 2018 году и её фейсбучного варианта F14. Обе основаны на принципе SIMD, который обеспечивает параллелизм на уровне данных.

Эти алгоритмы проверяют загруженность ячеек и совпадения «тега» элемента блоками по восемь слотов. Поэтому на любых разумных загрузках таблиц (до 90%) цепочка проверки очень редко превышает 1 (то есть, одну проверку 8-элементного блока). Соответственно, улучшения в «алгоритме шагания» просто не играют никакой роли, объясняет Левентов.

То есть на практике сейчас именно SwissTable считаются самыми быстрыми хеш-таблицами (это стандартный алгоритм в Rust и в свежем Golang 1.24), и новые алгоритмы Крапивина и др. не меняют данного факта.

Однако есть мнение, что на новом алгоритме всё-таки можно построить более быстрые хеш-таблицы, чем SwissTable.

P. S. 16 февраля 2025 года на сайте ArXiv.org опубликована ещё одна статья «Модель туалета: реалистичный подход к оптимизации алгоритмов хеш-таблиц» (The Bathroom Model: A Realistic Approach to Hash Table Algorithm Optimization) с описанием нового метода оптимизации поиска в хеш-таблицах, «вдохновлённого поведением людей реальном мире при выборе свободной кабинки в оживлённом общественном туалете»:

Иллюстрация из научной статьи

«В типичном сценарии человек использует стратегию последовательного или случайного поиска. В обычных условиях, когда большинство кабинок не занято, простой выбор по принципу „первая свободная“ работает эффективно. Однако на пиковых нагрузках проверка всех кабинок по очереди может быть неэффективной и отнимать много времени. Более эффективная стратегия предполагает динамическую настройку поиска на основе предварительной информации о занятости кабинок», — пишут авторы. Таким образом, метод динамически корректирует стратегию поиска на основе предварительных знаний о заполненности хеш-таблицы. Авторы формализовали свою модель, написали код и сравнили с существующими методами:

Сравнение эффективности поиска в хеш-таблице

Сравнение сложности зондирования в наихудшем случае

Пример кода

import numpy as np
import matplotlib.pyplot as plt
import sys

# Hash table size
TABLE_SIZE = 10000
LOAD_FACTORS = np.linspace(0.1, 0.95, 10)  # Varying load factors
NUM_KEYS = [int(TABLE_SIZE * load) for load in LOAD_FACTORS]

# Hash table methods
METHODS = ["Random Probing", "Elastic Hashing", "Funnel Hashing", "Bathroom Model"]

# Results storage
average_lookup_time = {method: [] for method in METHODS}
worst_case_probes = {method: [] for method in METHODS}
memory_utilization = {method: [] for method in METHODS}
MAX_PROBES = 100  # Prevent infinite loops

def hash_function(key, size=TABLE_SIZE):
    """Simple hash function for simulation purposes"""
    return key % size

def get_memory_usage(table):
    """Estimate memory usage of the hash table (in bytes)"""
    return sys.getsizeof(table) + sum(sys.getsizeof(item) for item in table if item is not None)

def random_probing(table, key):
    """Traditional random probing method"""
    index = int(hash_function(key))
    probes = 1  # Start with first probe attempt
    while table[index] is not None and probes < MAX_PROBES:
        index = (index + np.random.randint(1, TABLE_SIZE)) % TABLE_SIZE
        probes += 1
    table[index] = key if table[index] is None else table[index]  # Avoid overwriting
    return probes

def elastic_hashing(table, key):
    """Elastic hashing method based on the paper"""
    index = int(hash_function(key))
    probes = 1  # Start with first probe attempt
    jump = 1
    while table[index] is not None and probes < MAX_PROBES:
        index = (index + jump) % TABLE_SIZE
        jump *= 2  # Exponential step increase
        probes += 1
    table[index] = key if table[index] is None else table[index]
    return probes

def funnel_hashing(table, key):
    """Funnel hashing method, dividing table into decreasing size regions"""
    index = int(hash_function(key))
    probes = 1  # Start with first probe attempt
    sub_table_size = TABLE_SIZE
    while table[index] is not None and probes < MAX_PROBES:
        sub_table_size = max(2, sub_table_size // 2)  # Ensure sub_table_size is at least 2
        index = (index + np.random.randint(1, sub_table_size)) % TABLE_SIZE
        probes += 1
    table[index] = key if table[index] is None else table[index]
    return probes

def bathroom_model(table, key):
    """Bathroom Model: Adaptive dynamic probing"""
    index = int(hash_function(key))
    probes = 1  # Start with first probe attempt
    step_size = 1  # Start with a small step
    while table[index] is not None and probes < MAX_PROBES:
        step_size = min(step_size * 2, TABLE_SIZE // 4)  # Adaptive step growth
        index = (index + step_size) % TABLE_SIZE
        probes += 1
    table[index] = key if table[index] is None else table[index]
    return probes

# Running experiments
for num_keys in NUM_KEYS:
    for method in METHODS:
        table = [None] * TABLE_SIZE
        probes_list = []
        keys = np.random.randint(1, 10**6, num_keys).tolist()  # Convert to list for integer indexing
        for key in keys:
            if method == "Random Probing":
                probes_list.append(random_probing(table, key))
            elif method == "Elastic Hashing":
                probes_list.append(elastic_hashing(table, key))
            elif method == "Funnel Hashing":
                probes_list.append(funnel_hashing(table, key))
            elif method == "Bathroom Model":
                probes_list.append(bathroom_model(table, key))
        
        average_lookup_time[method].append(np.mean(probes_list))
        worst_case_probes[method].append(np.max(probes_list))
        memory_utilization[method].append(get_memory_usage(table))  # Record memory usage

# Plot results
plt.figure(figsize=(10, 5))
for method in METHODS:
    plt.plot(NUM_KEYS, average_lookup_time[method], label=method, marker='o')
plt.xlabel("Number of Keys Inserted")
plt.ylabel("Average Lookup Time")
plt.title("Comparison of Hash Table Lookup Efficiency")
plt.legend()
plt.grid()
plt.show()

plt.figure(figsize=(10, 5))
for method in METHODS:
    plt.plot(NUM_KEYS, worst_case_probes[method], label=method, marker='o')
plt.xlabel("Number of Keys Inserted")
plt.ylabel("Worst-Case Probe Complexity")
plt.title("Comparison of Worst-Case Probing")
plt.legend()
plt.grid()
plt.show()

plt.figure(figsize=(10, 5))
for method in METHODS:
    plt.plot(NUM_KEYS, memory_utilization[method], label=method, marker='o')
plt.xlabel("Number of Keys Inserted")
plt.ylabel("Memory Utilization (bytes)")
plt.title("Comparison of Memory Utilization Across Methods")
plt.legend()
plt.grid()
plt.show()

Telegram-канал со скидками, розыгрышами призов и новостями IT 💻