https://habr.com/ru/post/456738/- Python
- Программирование
- Машинное обучение
- Искусственный интеллект
Примечание

Перед вами – перевод свободной онлайн-книги Майкла Нильсена «Neural Networks and Deep Learning», распространяемой под лицензией
Creative Commons Attribution-NonCommercial 3.0 Unported License. Мотивацией к его созданию послужил успешный опыт перевода учебника по программированию, "
Выразительный JavaScript". Книга по нейросетям тоже достаточно популярна, на неё активно ссылаются авторы англоязычных статей. Её переводов я не нашёл, за исключением
перевода начала первой главы с сокращениями.
Желающие отблагодарить автора книги могут сделать это на её
официальной странице, переводом через PayPal или биткоин. Для поддержки переводчика на Хабре есть форма «поддержать автора».
Введение
Этот учебник подробно расскажет вам о таких понятиях, как:
- Нейросети — прекрасная программная парадигма, созданная под влиянием биологии, и позволяющая компьютеру учиться на основе наблюдений.
- Глубокое обучение – мощный набор техник обучения нейросетей.
Нейросети (НС) и глубокое обучение (ГО) на сегодня дают наилучшее решение многих задач из областей распознавания изображений, голоса и обработки естественного языка. Этот учебник научит вас многим ключевым концепциям, лежащим в основе НС и ГО.
О чём эта книга
НС – одна из прекраснейших программных парадигм, когда-либо придуманных человеком. При стандартном подходе к программированию мы сообщаем компьютеру, что делать, разбиваем большие задачи на множество малых, точно определяем задачи, которые компьютеру будет легко исполнить. В случае с НС мы, наоборот, не говорим компьютеру, как решать задачу. Он сам обучается этому на основе «наблюдений» за данными, «придумывая» собственное решение поставленной задачи.
Автоматическое обучение на основе данных звучит многообещающе. Однако до 2006 года мы не знали, как обучать НС так, чтобы они могли превзойти более традиционные подходы, за исключением нескольких особых случаев. В 2006 были открыты техники обучения т.н. глубоких нейросетей (ГНС). Теперь эти техники известны, как глубокое обучение (ГО). Их продолжали разрабатывать, и сегодня ГНС и ГО достигли потрясающих результатов во многих важных задачах, связанных с компьютерным зрением, распознаванием речи и обработки естественного языка. В крупных масштабах их развёртывают такие компании, как Google, Microsoft и Facebook.
Цель этой книги – помочь вам овладеть ключевыми концепциями нейросетей, включая и современные техники ГО. Поработав с учебником, вы напишете код, использующий НС и ГО для решения сложных задач распознавания закономерностей. У вас появится фундамент для использования НС и ГО в подходе к решению собственных задач.
Подход с упором на принципы
Одно из убеждений, лежащих в основе книги, состоит в том, что лучше овладеть твёрдым пониманием ключевых принципов НС и ГО, чем нахватать знаний из длинного списка различных идей. Если вы хорошо разберётесь в ключевых идеях, вы быстро поймёте и другой новый материал. На языке программиста можно сказать, что мы будем изучать основной синтаксис, библиотеки и структуры данных нового языка. Возможно, вы узнаете лишь малую долю всего языка – у многих языков есть необъятные стандартные библиотеки – однако новые библиотеки и структуры данных вы сможете понимать быстро и легко.
Так что, эта книга категорически не является обучающим материалом по тому, как использовать какую-то определённую библиотеку для НС. Если вы хотите просто научиться работать с библиотекой – не читайте книгу! Найдите нужную библиотеку, и работайте с обучающими материалами и документацией. Но имейте в виду: хотя у такого подхода есть преимущество в мгновенном решении задачи, если вы хотите понять, что конкретно происходит внутри НС, если вы хотите овладеть идеями, которые будут актуальны и через много лет, тогда вам недостаточно будет просто изучить какую-то модную библиотеку. Вам нужно понять надёжные и долгосрочные идеи, лежащие в основе работы НС. Технологии приходят и уходят, а идеи – вечны.
Практический подход
Мы изучим основные принципы на примере конкретной задачи: обучения компьютеру распознавания рукописных цифр. Используя традиционные подходы к программированию, такую задачу решить чрезвычайно тяжело. Однако мы сможем достаточно неплохо решить её при помощи простой НС и нескольких десятков строчек кода, без всяких специальных библиотек. Более того, мы будем постепенно улучшать эту программу, последовательно включая в неё всё больше и больше ключевых идей о НС и ГО.
Такой практический подход означает, что вам потребуется некий опыт в программировании. Но вам не обязательно быть профессиональным программистом. Я написал код на python (версии 2.7), который должен быть понятным, даже если вы не писали программ на python. В процессе изучения мы создадим свою библиотечку для НС, которую вы сможете использовать для экспериментов и дальнейшего обучения. Весь код можно
скачать по ссылке. Закончив книгу, или в процессе чтения, вы сможете выбрать одну из более завершённых библиотек для НС, приспособленных для использования в настоящих проектах.
Математические требования для понимания материала довольно средние. В большинстве глав есть математические части, но обычно это элементарная алгебра и графики функций. Иногда я использую более продвинутую математику, но я структурировал материал так, чтобы вы смогли понимать его, даже если некие детали будут ускользать от вас. Больше всего математики используется в главе 2, где требуется немного матанализа и линейной алгебры. Для тех, кому они не знакомы, я начинаю главу 2 с введения в математику. Если она покажется вам сложной, просто пропустите главу вплоть до подведения итогов. В любом случае, волноваться по этому поводу не стоит.
Книга редко бывает одновременно ориентированной на понимание принципов и практический подход. Но я считаю, что лучше учиться на основе фундаментальных идей НС. Мы будем писать рабочий код, а не только изучать абстрактную теорию, и этот код вы сможете исследовать и расширять. Таким способом вы поймёте основы, как теории, так и практики, и будете способны учиться дальше.
Упражнения и задачи
Авторы технических книг часто предупреждают читателя о том, что ему просто необходимо выполнять все упражнения и решать все задачи. При чтении подобных предупреждений мне они всегда кажутся немного странными. Неужто со мной произойдёт что-то плохое, если я не буду выполнять упражнения и решать задачи? Нет, конечно. Я просто сэкономлю время за счёт менее глубокого понимания. Иногда оно того стоит. Иногда нет.
Что стоит делать с этой книгой? Советую попытаться выполнить большинство упражнений, но не пытайтесь решать большинство задач.
Выполнить большинство упражнений нужно потому, что это – базовые проверки правильного понимания материала. Если вы не можете с относительной лёгкостью выполнить упражнение, вы, наверное, упустили что-то фундаментальное. Конечно, если вы прямо-таки застрянете на каком-то упражнении – бросайте его, может быть, это какое-то небольшое недопонимание, или, возможно, я что-то плохо сформулировал. Но если большинство упражнений вызывает у вас затруднения, тогда вам, скорее всего, надо перечитать предыдущий материал.
Задачи – дело другое. Они сложнее упражнений, и с некоторыми вам придётся тяжело. Это раздражает, но, конечно, терпение перед лицом такого разочарования – это единственный способ по-настоящему понять и усвоить предмет.
Так что я не рекомендую решать все задачи. Ещё лучше – подобрать собственный проект. Может, вы захотите использовать НС для классификации своей коллекции музыки. Или для предсказания стоимости акций. Или чего-то ещё. Но найдите интересный вам проект. И потом вы сможете игнорировать задачи из книги, или использовать их чисто как вдохновение для работы над вашим проектом. Проблемы с собственным проектом научат вас большему, чем работа с любым количеством задач. Эмоциональное вовлечение – ключевой фактор в достижении мастерства.
Конечно, пока у вас может и не быть такого проекта. Это нормально. Решайте задачи, для которых вы чувствуете внутреннюю мотивацию. Используйте материал из книги, чтобы помочь себе в поиске идей для личных творческих проектов.
Глава 1
Зрительная система человека – одно из чудес света. Рассмотрим следующую последовательность рукописных цифр:

Большинство людей без труда прочтут их, как 504192. Но эта простота обманчива. В каждом полушарии мозга у человека есть первичная
зрительная кора, также известная, как V1, в которой содержится 140 млн нейронов и десятки миллиардов связей между ними. При этом в зрении человека участвует не только V1, но целая последовательность участков мозга — V2, V3, V4 и V5 – которые занимаются всё более сложной обработкой изображений. Мы носим в своей голове суперкомпьютер, настроенный эволюцией в течение сотен миллионов лет, и прекрасно адаптированный для понимания видимого мира. Распознавать рукописные цифры не так-то легко. Просто мы, люди, потрясающе, удивительно хорошо распознаём то, что показывают нам наши глаза. Но почти вся эта работа проводится бессознательно. И обычно мы не придаём значения тому, какую сложную задачу решают наши зрительные системы.
Сложность распознавания зрительных закономерностей становится очевидной, когда вы пытаетесь написать компьютерную программу для распознавания таких цифр, как приведённые выше. То, что кажется лёгким в нашем исполнении, внезапно оказывается чрезвычайно сложным. Простое понятие о том, как мы распознаём формы – «у девятки сверху петля, и вертикальная чёрточка справа внизу»- оказывается вовсе не таким простым для алгоритмического выражения. Пытаясь сформулировать эти правила чётко, вы быстро вязнете в трясине исключений, подводных камней и особых случаев. Задача кажется безнадёжной.
НС подходят к решению задачи по-другому. Идея в том, чтобы взять множество рукописных цифр, известных, как обучающие примеры,

и разработать систему, способную обучаться на этих примерах. Иначе говоря, НС использует примеры для автоматического построения правил распознавания рукописных цифр. Более того, увеличивая количество обучающих примеров, сеть может больше узнать о рукописных цифрах и улучшить свою точность. Так что, хотя я привёл выше всего 100 обучающих примеров, возможно, мы сможем создать более хороший распознаватель рукописных цифр, используя тысячи или даже миллионы и миллиарды обучающих примеров.
В этой главе мы напишем компьютерную программу, реализующую НС, обучающуюся распознавать рукописные цифры. Программа будет всего в 74 строки длиной, и не будет использовать специальных библиотек для НС. Однако эта короткая программа сможет распознавать рукописные цифры с точностью более 96%, не требуя вмешательства человека. Более того, в дальнейших главах мы разработаем идеи, способные улучшить точность до 99% и более. На самом деле лучшие коммерческие НС настолько хорошо справляются с задачей, что используются банками для обработки чеков, и почтовой службой – для распознавания адресов.
Мы концентрируемся на распознавании рукописного текста, поскольку это прекрасный прототип задачи для изучения НС. Такой прототип идеально подходит для нас: это сложная задача (распознать рукописные цифры – дело непростое), но не настолько сложная, чтобы для неё требовалось чрезвычайно сложное решение или необъятные вычислительные мощности. Более того, это прекрасный способ для разработки более сложных техник, таких, как ГО. Поэтому в книге мы будем постоянно возвращаться к задаче распознавания рукописного текста. Позже мы обсудим, как эти идеи можно применить к другим задачам компьютерного зрения, к распознаванию речи, обработке естественного языка и другим областям.
Конечно, если бы целью этой главы было только написать программу распознавания рукописных цифр, то глава была бы куда короче! Однако в процессе мы выработаем много ключевых идей, связанных с НС, включая два важных типа искусственного нейрона (
перцептрон и сигмоидный нейрон), и стандартный алгоритм обучения НС,
стохастический градиентный спуск. В тексте я концентрируюсь на том, чтобы объяснить, почему всё делается именно так, и на формировании вашего понимания НС. Для этого требуется более долгий разговор, чем если бы я просто представил базовую механику происходящего, однако это стоит более глубокого понимания, которое возникнет у вас. Среди других преимуществ – к концу главы вы поймёте, что такое ГО и почему оно так важно.
Перцептроны
Что такое нейросеть? Для начала я расскажу об одном типе искусственного нейрона, который называется перцептрон. Перцептроны придумал в 1950-60-х учёный
Фрэнк Розенблатт, вдохновившись ранней работой
Уоррена Мак-Каллока и
Уолтера Питтса. Сегодня чаще используются другие модели искусственных нейронов – в данной книге, и большинстве современных работ по НС в основном используют сигмоидную модель нейрона. Мы вскоре с ней познакомимся. Но чтобы понять, почему сигмоидные нейроны определяются именно так, стоит потратить время на разбор перцептрона.
Так как же работают перцептроны? Перцептрон принимает на вход несколько двоичных чисел x
1,x
2,… и выдаёт одно двоичное число:
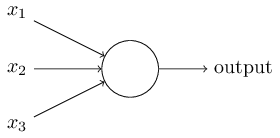
В данном примере у перцептрона есть три числа на входе, x
1, x
2, x
3. В общем случае их может быть больше или меньше. Розенблатт предложил простое правило для вычисления результата. Он ввёл веса, w
1, w
2, вещественные числа, выражающие важность соответствующих входных чисел для результатов. Выход нейрона, 0 или 1, определяется тем, меньше или больше некоего порога [threshold] взвешенная сумма
. Как и веса, порог – вещественное число, параметр нейрона. Говоря математическими терминами:
Вот и всё описание работы перцептрона!
Такова базовая математическая модель. Перцептрон можно представить себе, как устройство, принимающее решение, взвешивая свидетельства. Приведу не очень реалистичный, но простой пример. Допустим, наступают выходные, и вы слышали, что в вашем городе пройдёт фестиваль сыра. Вы любите сыр, и пытаетесь решить, идти ли на фестиваль, или нет. Вы можете принять решение, взвесив три фактора:
- Хорошая ли погода?
- Хочет ли идти с вами ваш партнёр?
- Далеко ли фестиваль от остановки общественного транспорта? (Машины у вас нет).
Три этих фактора можно представить двоичными переменными x
1, x
2, x
3. К примеру, x
1 = 1, если погода хорошая, а 0 – если плохая. x
2 = 1, если ваш партнёр хочет пойти, и 0 – если нет. То же для x
3.
Теперь, допустим, вы фанатеете от сыра настолько, что готовы ехать на фестиваль, даже если вашего партнёра это не интересует, и до него трудно добраться. Но, возможно, вы просто ненавидите плохую погоду, и в случае непогоды на фестиваль не пойдёте. Вы можете использовать перцептроны для моделирования такого процесса принятия решения. Один из способов – выбрать вес w
1 = 6 для погоды, и w
2 = 2, w
3 = 2 для других условий. Большее значение w
1 говорит о том, что погода имеет для вас значение гораздо большее, чем то, присоединится ли к вам ваш партнёр, или близость фестиваля к остановке. Наконец, допустим, вы выбираете для перцептрона порог 5. С такими вариантами перцептрон реализует нужную модель принятия решений, выдавая 1, когда погода хорошая, и 0, когда она плохая. Желание партнёра и близость остановки не влияют на выходное значение.
Изменяя веса и порог, мы можем получить разные модели принятия решений. К примеру, допустим, возьмём порог 3. Тогда перцептрон решит, что вам нужно идти на фестиваль, либо когда погода хорошая, либо когда фестиваль находится рядом с остановкой и ваш партнёр согласен идти с вами. Иначе говоря, модель получается другой. Понижение порога означает, что вам больше хочется пойти на фестиваль.
Очевидно, перцептрон не является полной моделью принятия решений человеком! Но этот пример показывает, как перцептрон может взвешивать разные виды свидетельств, чтобы принимать решения. Кажется возможным, что сложная сеть перцептронов может принимать весьма сложные решения:
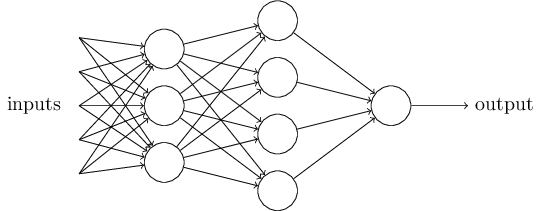
В этой сети первый столбец перцептронов – то, что мы называем первым слоем перцептронов – принимает три очень простых решения, взвешивая входные свидетельства. Что насчёт перцептронов из второго слоя? Каждый из них принимает решение, взвешивая результаты первого слоя принятия решений. Таким способом перцептрон второго слоя может принять решение на более сложном и абстрактном уровне, по сравнению с перцептроном первого слоя. А ещё более сложные решения могут принимать перцептроны на третьем слое. Таким способом многослойная сеть перцептронов может заниматься принятием сложных решений.
Кстати, когда я определял перцептрон, я сказал, что у него есть только одно выходное значение. Но в сети наверху перцептроны выглядят так, будто у них есть несколько выходных значений. На самом деле, выход у них только один. Множество выходных стрелок – просто удобный способ показать, что выход перцептрона используется как вход нескольких других перцептронов. Это менее громоздко, чем рисовать один разветвляющийся выход.
Давайте упростим описание перцептронов. Условие
неуклюжее, и мы можем договориться о двух изменениях записи для её упрощения. Первое – записывать
как скалярное произведение,
, где w и x – вектора, компонентами которых служат веса и входные данные, соответственно. Второе – перенести порог в другую часть неравенства, и заменить его значением, известным, как смещение перцептрона [bias],
. Используя смещение вместо порога, мы можем переписать правило перцептрона:
Смещение можно представлять, как меру того, насколько легко получить от перцептрона значение 1 на выходе. Или, в биологических терминах, смещение – мера того, насколько просто заставить перцептрон активироваться. Перцептрону с очень большим смещением крайне легко выдать 1. Но с очень большим отрицательным смещением это сделать трудно. Очевидно, введение смещения – это небольшое изменение в описании перцептронов, однако позднее мы увидим, что оно приводит к дальнейшему упрощению записи. Поэтому далее мы не будем использовать порог, а всегда будем использовать смещение.
Я описал перцептроны с точки зрения метода взвешивания свидетельств с целью принятия решения. Ещё один метод их использования – вычисление элементарных логических функций, которые мы обычно считаем основными вычислениями, таких, как AND, OR и NAND. Допустим, к примеру, что у нас есть перцептрон с двумя входами, вес каждого из которых равен -2, а его смещение равно 3. Вот он:
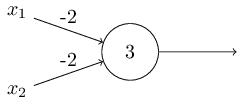
Входные данные 00 дают на выходе 1, поскольку (−2)∗0+(−2)∗0+3=3 больше нуля. Те же вычисления говорят, что входные данные 01 и 10 дают 1. Но 11 на входе даёт 0 на выходе, поскольку (−2)∗1+(−2)∗1+3=−1, меньше нуля. Поэтому наш перцептрон реализует функцию NAND!
Этот пример показывает, что можно использовать перцептроны для вычисления базовых логических функций. На самом деле, мы можем использовать сети перцептронов для вычисления вообще любых логических функций. Дело в том, что
логический вентиль NAND универсален для вычислений – на его основе можно строить любые вычисления. К примеру, можно использовать вентили NAND для создания контура, складывающего два бита, x
1 и x
2. Для этого нужно вычислить побитовую сумму
, а также
флаг переноса, который равняется 1, когда оба x
1 и x
2 равны 1 – то есть, флаг переноса является просто результатом побитового умножения x
1x
2:
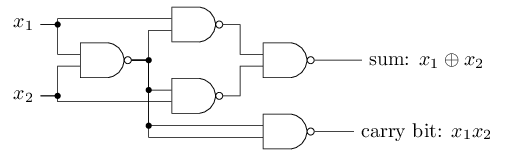
Чтобы получить эквивалентную сеть из перцептронов, мы заменяем все вентили NAND перцептронами с двумя входами, вес каждого из которых равен -2, и со смещением 3. Вот получившаяся сеть. Отметьте, что я передвинул перцептрон, соответствующий правому нижнему вентилю, просто чтобы было удобнее рисовать стрелочки:
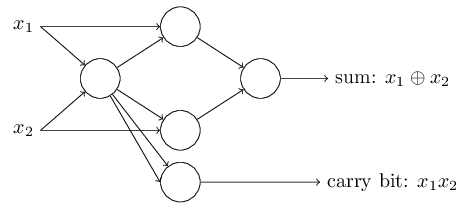
Один примечательный аспект данной сети из перцептронов – выходные данные самого левого из них используются дважды как входные для нижнего. Определяя модель перцептрона, я не упоминал о допустимости подобной схемы двойного выхода в одно и то же место. На самом деле, это не имеет большого значения. Если мы не хотим позволять такое, мы можем просто объединить две линии с весами в -2 в одну с весом -4. (Если это не кажется вам очевидным, остановитесь, и докажите это себе). После этого изменения сеть выглядит следующим образом, причём все неразмеченные веса равны -2, все смещения равны 3, а один вес -4 отмечен:
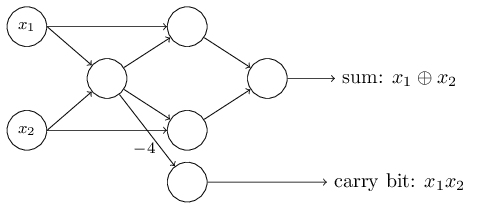
Такая запись перцептронов, у которых есть выход, но нет входов:
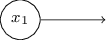
является просто сокращением. Это не значит, что у него нет входов. Чтобы понять это, допустим, что у нас есть перцептрон без входов. Тогда взвешенная сумма ∑
jw
jx
j была бы всегда равной нулю, поэтому перцептрон выдавал бы 1 при b > 0 и 0 при b ≤ 0. То есть, перцептрон просто выдавал бы фиксированное значение, а не необходимое нам (x
1 в примере выше). Лучше считать входные перцептроны не перцептронами, а особыми единицами, которые просто определены так, чтобы выдавать нужные значения x
1, x
2,…
Пример с сумматором демонстрирует, как можно использовать сеть из перцептронов для симуляции контура, содержащего множество вентилей NAND. А поскольку эти вентили универсальны для вычислений, следовательно, и перцептроны универсальны для вычислений.
Вычислительная универсальность перцептронов одновременно обнадёживает и разочаровывает. Обнадёживает она, гарантируя, что сеть из перцептронов может быть настолько же мощной, насколько любое другое вычислительное устройство. Разочаровывает, создавая впечатление, что перцептроны – всего лишь новый тип логического вентиля NAND. Так себе открытие!
Однако на самом деле ситуация лучше. Оказывается, что мы можем разработать обучающие алгоритмы, способные автоматически подстраивать веса и смещения сети из искусственных нейронов. Эта подстройка происходит в ответ на внешние стимулы, без прямого вмешательства программиста. Эти обучающие алгоритмы позволяют нам использовать искусственные нейроны способом, радикально отличным от обычных логических вентилей. Вместо того, чтобы явно прописывать контур из вентилей NAND и других, наши нейросети могут просто обучиться решать задачи, иногда такие, для которых было бы чрезвычайно сложно напрямую спроектировать обычный контур.
Сигмоидные нейроны
Обучающие алгоритмы – это прекрасно. Однако как разработать такой алгоритм для нейросети? Допустим, у нас есть сеть перцептронов, которую мы хотим использовать для обучения решения задачи. Допустим, входными данными сети могут быть пиксели отсканированного изображения рукописной цифры. И мы хотим, чтобы сеть узнала веса и смещения, необходимые для правильной классификации цифры. Чтобы понять, как может работать такое обучение, представим, что мы немного меняем некий вес (или смещение) в сети. Мы хотим, чтобы это небольшое изменение привело к небольшому изменению выходных данных сети. Как мы скоро видим, это свойства делает возможным обучение. Схематично мы хотим следующего (очевидно, такая сеть слишком проста, чтобы распознавать рукописный ввод!):
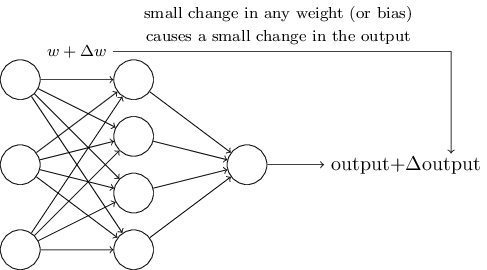
Если бы небольшое изменение веса (или смещения) приводило бы к небольшому изменению результата на выходе, мы могли бы изменять веса и смещения, чтобы наша сеть вела себя чуть ближе к желаемому. К примеру, допустим, что сеть неправильно отнесла изображение к «8», хотя должна была к «9». Мы могли бы разобраться, как внести небольшое изменение в веса и смещения, чтобы сеть немного ближе подобралась к классификации изображения, как «9». А потом мы бы повторяли это, изменяя веса и смещения снова и снова, чтобы получать всё лучший и лучший результат. Сеть бы училась.
Проблема в том, что если в сети есть перцептроны, такого не происходит. Небольшое изменение весов или смещения любого перцептрона иногда может привести к изменению его выхода на противоположный, допустим, с 0 на 1. Такой переворот может изменить поведение остальной сети очень сложным образом. И даже если теперь наша «9» и будет правильно распознана, поведение сети со всеми остальными изображениями, вероятно, полностью изменилось таким образом, который сложно контролировать. Из-за этого сложно представить, как можно постепенно подстраивать веса и смещения, чтобы сеть постепенно приближалась к желаемому поведению. Возможно, существует некий хитроумный способ обойти эту проблему. Но нет никакого простого решения задачи обучения сети из перцептронов.
Эту проблему можно обойти, введя новый тип искусственного нейрона под названием сигмоидный нейрон. Они похожи на перцептроны, но изменены так, чтобы небольшие изменения весов и смещений приводили только к небольшим изменениям выходных данных. Это основной факт, который позволит сети из сигмоидных нейронов обучаться.
Давайте я опишу сигмоидный нейрон. Рисовать мы их будем так же, как перцептроны:
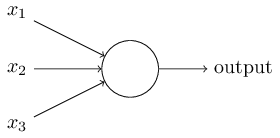
У него точно так же есть входные данные x
1, x
2,… Но вместо того, чтобы приравниваться к 0 или 1, эти входы могут иметь любое значение в промежутке от 0 до 1. К примеру, величина 0,638 будет допустимым значением входных данных для сигмоидного нейрона (СН). Так же, как у перцептрона, у СН есть веса для каждого входа, w
1, w
2,… и общее смещение b. Но его выходным значением будет не 0 или 1. Это будет σ(w⋅x+b), где σ — это сигмоида.
Кстати, σ иногда называют
логистической функцией, а этот класс нейронов – логистическими нейронами. Эту терминологию полезно запомнить, поскольку эти термины используют многие люди, работающие с нейросетями. Однако мы будем придерживаться сигмоидной терминологии.
Определяется функция так:
В нашем случае выходное значение сигмоидного нейрона с входными данными x
1, x
2,… весами w
1, w
2,… и смещением b будет считаться, как:
На первый взгляд, СН кажутся совсем не похожими на нейроны. Алгебраический вид сигмоиды может показаться запутанным и малопонятным, если вы с ним не знакомы. На самом деле между перцептронами и СН есть много общего, и алгебраическая форма сигмоиды оказывается больше технической подробностью, нежели серьёзным барьером к пониманию.
Чтобы понять сходство с моделью перцептрона, допустим, что z ≡ w ⋅ x + b – большое положительное число. Тогда e – z ≈ 0, поэтому σ(z) ≈ 1. Иначе говоря, когда z = w ⋅ x + b большое и положительное, выход СН примерно равен 1, как у перцептрона. Допустим, что z = w ⋅ x + b большое со знаком минус. Тогда e – z → ∞, а σ(z) ≈ 0. Так что при больших z со знаком минус поведение СН тоже приближается к перцептрону. И только когда w ⋅ x + b имеет средний размер, наблюдаются серьёзные отклонения от модели перцептрона.
Что насчёт алгебраического вида σ? Как нам его понять? На самом деле, точная форма σ не так уж важна – важна форма функции на графике. Вот она:
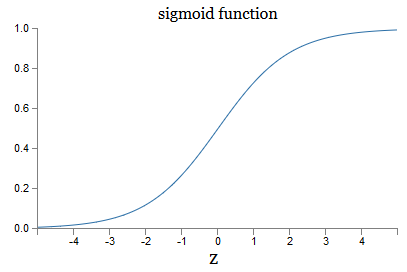
Это сглаженный вариант ступенчатой функции:
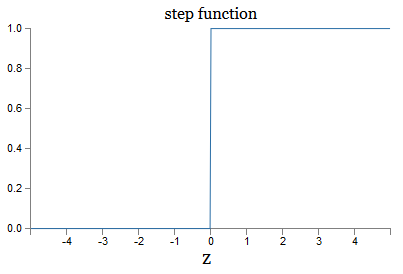
Если бы σ была ступенчатой, тогда СН был бы перцептроном, поскольку у него на выходе наблюдались бы 0 или 1 в зависимости от знака w ⋅ x + b (ну, на самом деле при z = 0 перцептрон выдаёт 0, а ступенчатая функция – 1, так что в одной этой точке функцию пришлось бы поменять).
Используя реальную функцию σ, мы получаем сглаженный перцептрон. И главным тут является гладкость функции, а не её точная форма. Гладкость означает, что небольшие изменения Δw
j весов и δb смещений дадут небольшие изменения Δoutput выходных данных. Алгебра говорит нам, что Δoutput хорошо аппроксимируется так:
Где суммирование идёт по всем весам w
j, а ∂output/∂w
j и ∂output/∂b обозначают частные производные выходных данных по w
j и b соответственно. Не паникуйте, если чувствуете себя неуверенно в компании частных производных! Хотя формула и выглядит сложной, со всеми этими частными производными, на самом деле она говорит нечто совсем простое (и полезное): Δoutput – это линейная функция, зависящая от Δw
j и Δb весов и смещения. Её линейность облегчает выбор небольших изменений весов и смещений для достижения любого желаемого небольшого смещения выходных данных. Так что, хотя по качественному поведению СН похожи на перцептроны, они облегчают понимание того, как можно изменить выход, меняя веса и смещения.
Если для нас имеет значение общая форма σ, а не её точный вид, то почему мы используем именно такую формулу (3)? На самом деле позднее мы иногда будем рассматривать нейроны, выход которых равняется f(w ⋅ x + b), где f() – некая другая функция активации. Главное, что меняется при смене функции – значения частных производных в уравнении (5). Оказывается, что когда мы потом подсчитываем эти частные производные, использование σ сильно упрощает алгебру, поскольку у экспонент есть очень приятные свойства при дифференцировании. В любом, случае, σ часто используется в работе с нейросетями, и чаще всего в этой книге мы будем использовать такую функцию активации.
Как интерпретировать результат работы СН? Очевидно, главным различием между перцептронами и СН будет то, что СН не выдают только 0 или 1. Их выходными данными может быть любое вещественное число от 0 до 1, так что значения типа 0,173 или 0,689 являются допустимыми. Это может быть полезно, к примеру, если вам нужно, чтобы выходное значение обозначало, к примеру, среднюю яркость пикселей изображения, поступившего на вход НС. Но иногда это может быть неудобно. Допустим, мы хотим, чтобы выход сети говорил о том, что «на вход поступило изображение 9» или «входящее изображение не 9». Очевидно, проще было бы, если бы выходные значения были 0 или 1, как у перцептрона. Но на практике мы можем договориться, что любое выходное значение не меньше 0,5 обозначало бы «9» на входе, а любое значение меньше 0,5, обозначало бы, что это «не 9». Я всегда буду явно указывать на наличие подобных договорённостей.
Упражнения
- СН, симулирующие перцептроны, часть 1
Допустим, мы берём все веса и смещения из сети перцептронов, и умножаем их на положительную константу c>0. Покажите, что поведение сети не изменяется.
- СН, симулирующие перцептроны, часть 2
Допустим, у нас та же ситуация, что в прошлой задаче – сеть перцептронов. Также допустим, что выбраны входные данные для сети. Конкретное значение нам не нужно, главное, что оно фиксировано. Допустим, веса и смещения таковы, что w⋅x+b ≠ 0, где x – входное значение любого перцептрона сети. Теперь заменим все перцептроны в сети на сН, и умножим веса и смещения на положительную константу c>0. Покажите, что в пределе c → ∞ поведение сети из СН будет ровно таким же, как сети перцептронов. Каким образом это утверждение будет нарушаться, если для одного из перцептронов w⋅x+b = 0?
Архитектура нейросетей
В следующем разделе я представлю нейросеть, способную на неплохую классификацию рукописных цифр. Перед этим полезно объяснить терминологию, позволяющую нам указывать на разные части сети. Допустим, у нас есть следующая сеть:
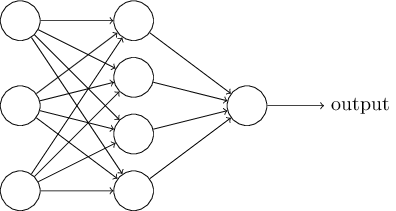
Как я уже упоминал, самый левый слой в сети называется входным слоем, а его нейроны – входными нейронами. Самый правый, или выходной слой, содержит выходные нейроны, или, как в нашем случае, один выходной нейрон. Средний слой называется скрытым, поскольку его нейроны не являются ни входными, ни выходными. Термин «скрытый», возможно, звучит немного загадочно – впервые услышав его, я решил, что у него должна быть некая глубокая философская или математическая важность – однако он означает лишь «не вход и не выход». У сети выше есть только один скрытый слой, но у некоторых сетей есть по нескольку скрытых слоёв. К примеру, в следующей четырёхслойной сети есть два скрытых слоя:
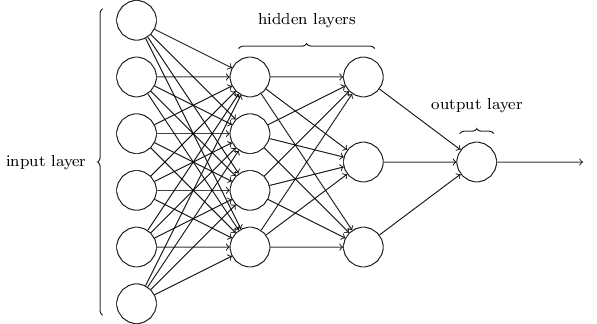
Это может сбивать с толку, но по историческим причинам такие сети с несколькими слоями иногда называют многослойными перцептронами, MLP, несмотря на то, что они состоят из сигмоидных нейронов, а не перцептронов. Я не собираюсь использовать такую терминологию, поскольку она сбивает с толку, но должен предупредить о её существовании.
Проектирование входных и выходных слоёв иногда является простой задачей. К примеру, допустим, мы пытаемся определить, означает ли рукописная цифра «9», или нет. Естественной схемой сети будет кодировать яркость пикселей изображения во входных нейронах. Если изображение будет чёрно-белым, размером 64х64 пикселя, тогда у нас будет 64х64=4096 входных нейронов, с яркостью в промежутке от 0 до 1. Выходной слой будет содержать всего один нейрон, чьё значение менее 0,5 будет означать, что «на входе была не 9», а значения более будут означать, что «на входе была 9».
И если проектирование входных и выходных слоёв часто является простой задачей, то проектирование скрытых слоёв может оказаться сложным искусством. В частности, невозможно описать процесс разработки скрытых слоёв при помощи нескольких простых практических правил. Исследователи НС разработали множество эвристических правил проектирования скрытых слоёв, помогающих получать нужное поведение нейросетей. К примеру, такую эвристику можно использовать, чтобы понять, как достичь компромисса между количеством скрытых слоёв и временем, доступным для обучения сети. Позднее мы столкнёмся с некоторыми из этих правил.
Пока что мы обсуждали НС, в которых выходные данные одного слоя используются в качестве входных для следующего. Такие сети называются нейросетями прямого распространения. Это значит, что в сети нет петель – информация всегда проходит вперёд, и никогда не скармливается назад. Если бы у нас были петли, мы бы встречали ситуации, в которых входные данные сигмоиды зависели бы от выходных. Это было бы тяжело осмыслить, и таких петель мы не допускаем.
Однако существуют и другие модели искусственных НС, в которых возможно использовать петли обратной связи. Эти модели называются
рекуррентными нейронными сетями (РНС). Идея этих сетей в том, что их нейроны активируются на ограниченные промежутки времени. Эта активация может стимулировать другие нейтроны, которые могут активироваться чуть позже, также на ограниченное время. Это приводит к активации следующих нейронов, и со временем мы получаем каскад активированных нейронов. Петли в таких моделях не представляют проблем, поскольку выход нейрона влияет на его вход в некий более поздний момент, а не сразу.
РНС были не такими влиятельными, как НС прямого распространения, в частности потому, что обучающие алгоритмы для РНС пока что обладают меньшими возможностями. Однако РНС всё равно остаются чрезвычайно интересными. По духу работы они гораздо ближе к мозгу, чем НС прямого распространения. Возможно, что РНС смогут решить важные задачи, которые при помощи НС прямого распространения решаются с большими сложностями. Однако чтобы ограничить область нашего изучения, мы сконцентрируемся на более широко применяемых НС прямого распространения.
Простая сеть классификации рукописных цифр
Определив нейросети, вернёмся к распознаванию рукописного текста. Задачу распознавания рукописных цифр мы можем разделить на две подзадачи. Сначала мы хотим найти способ разбиения изображения, содержащего много цифр, на последовательность отдельных изображений, каждое из которых содержит одну цифру. К примеру, мы хотели бы разбить изображение

на шесть отдельных

Мы, люди, с лёгкостью решаем эту задачу сегментации, однако для компьютерной программы сложно правильно разбить изображение. После сегментации программе нужно классифицировать каждую отдельную цифру. Так что, к примеру, мы хотим, чтобы наша программа распознала, что первая цифра
это 5.
Мы сконцентрируемся на создании программы для решения второй задачи, классификации отдельных цифр. Оказывается, что задачу сегментации решить не так сложно, как только мы найдём хороший способ классификации отдельных цифр. Для решения задачи сегментации есть множество подходов. Один из них – попробовать множество разных способов сегментации изображения с использованием классификатора отдельных цифр, оценивая каждую попытку. Пробная сегментация получает высокую оценку, если классификатор отдельных цифр уверен в классификации всех сегментов, и низкую, если у него есть проблемы в одном или нескольких сегментах. Идея в том, что если у классификатора где-то есть проблемы, это, скорее всего, означает, что сегментация проведена некорректно. Эту идею и другие варианты можно использовать для неплохого решения задачи сегментации. Так что, вместо того, чтобы беспокоиться по поводу сегментации, мы сконцентрируемся на разработке НС, способной решать более интересную и сложную задачу, а именно, распознавать отдельные рукописные цифры.
Для распознавания отдельных цифр мы будем использовать НС из трёх слоёв:
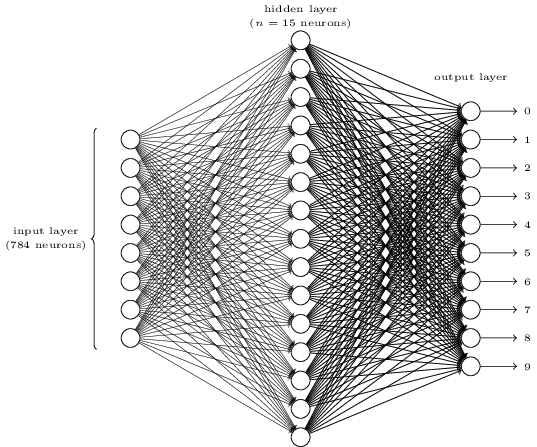
Входной слой сети содержит нейроны, кодирующие различные значения входных пикселей. Как будет указано в следующем разделе, наши обучающие данные будут состоять из множества изображений отсканированных рукописных цифр размера 28х28 пикселей, поэтому входной слой содержит 28х28=784 нейрона. Для простоты я не стал указывать большую часть из 784 нейронов на диаграмме. Входящие пиксели чёрно-белые, при этом значение 0,0 обозначает белый цвет, 1,0 обозначает чёрный, а промежуточные значения обозначают всё более тёмные оттенки серого.
Второй слой сети – скрытый. Мы обозначим количество нейронов в этом слое n, и будем экспериментировать с различными значениями n. На примере вверху показан небольшой скрытый слой, содержащий всего n=15 нейронов.
В выходном слое сети 10 нейронов. Если активируется первый нейрон, то есть, его выходное значение ≈ 1, это говорит о том, что сеть считает, что на входе был 0. Если активируется второй нейрон, сеть считает, что на входе был 1. И так далее. Строго говоря, мы нумеруем выходные нейроны от 0 до 9, и смотрим, у какого из них значение активации было максимальным. Если это, допустим, нейрон №6, тогда наша сеть считает, что на входе была цифра 6. И так далее.
Вы можете задуматься над тем, зачем нам использовать десять нейронов. Ведь мы же хотим узнать, какой цифре от 0 до 9 соответствует входное изображение. Естественно было бы использовать всего 4 выходных нейрона, каждый из которых принимал бы двоичное значение в зависимости от того, ближе его выходное значение к 0 или 1. Четырёх нейронов будет достаточно, поскольку 2
4=16, больше, чем 10 возможных значений. Зачем нашей сети использовать 10 нейронов? Это ведь неэффективно? Основание для этого эмпирическое; мы можем попробовать оба варианта сети, и окажется, что для данной задачи сеть с 10-ю выходными нейронами лучше обучается распознавать цифры, чем сеть с 4-мя. Однако остаётся вопрос, почему же 10 выходных нейронов лучше. Есть ли какая-то эвристика, которая заранее сказала бы нам, что следует использовать 10 выходных нейронов вместо 4?
Чтобы понять, почему, полезно подумать о том, что делает нейросеть. Рассмотрим сначала вариант с 10 выходными нейронами. Сконцентрируемся на первом выходном нейроне, который пытается решить, является ли входящее изображение нулём. Он делает это, взвешивая свидетельства, полученные из скрытого слоя. А что делают скрытые нейроны? Допустим, первый нейрон в скрытом слое определяет, есть ли на картинке что-то вроде такого:

Делать это он может, назначая большие веса пикселям, совпадающим с этим изображением, и малые веса остальным. Точно так же допустим, что второй, третий и четвёртый нейроны в скрытом слое ищут, есть ли на изображении подобные фрагменты:

Как вы могли догадаться, все вместе эти четыре фрагмента дают изображение 0, которое мы видели ранее:

Итак, если четыре скрытых нейрона активируются, мы можем заключить, что цифра равна 0. Конечно, это не единственное свидетельство того, что там был изображён 0 – мы можем получить 0 и множеством других способов (немного сдвигая указанные изображения или слегка искажая их). Однако можно точно сказать, что, по крайней мере, в этом случае мы можем заключить, что на входе был 0.
Если предположить, что сеть работает так, можно дать правдоподобное объяснение тому, почему лучше использовать 10 выходных нейронов вместо 4. Если бы у нас было 4 выходных нейрона, тогда первый нейрон пытался бы решить, каков самый старший бит у входящей цифры. И нет простого способа связать самый старший бит с простыми формами, приведёнными выше. Сложно представить какие-то исторические причины, по которым части формы цифры были бы как-то связаны с самым старшим битом выходных данных.
Однако всё вышесказанное подкрепляется только эвристикой. Ничто не говорит в пользу того, что трёхслойная сеть должна работать так, как я сказал, а скрытые нейроны должны находить простые компоненты форм. Возможно, хитрый алгоритм обучения найдёт какие-нибудь значения весов, которые позволят нам использовать только 4 выходных нейрона. Однако в качестве эвристики мой способ работает неплохо, и может сэкономить вам значительное время при разработке хорошей архитектуры НС.
Упражнения
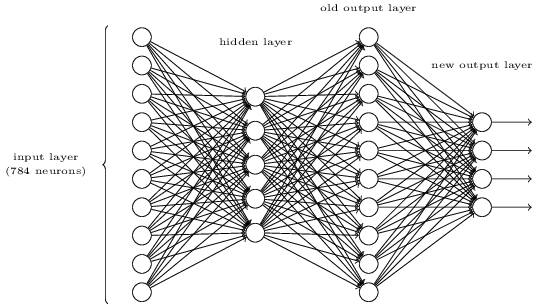
- Существует способ определить побитовое представление числа, добавив дополнительный слой к трёхслойной сети. Дополнительный слой преобразует выходные значения предыдущего слоя в двоичный формат, как показано на рисунке ниже. Найдите наборы весов и смещений для нового выходного слоя. Предполагаем, что первые 3 слоя нейронов таковы, что правильный выход с третьего слоя (бывший выходной слой) активируется значениями не менее 0,99, а неправильные выходные значения не превышают 0,01.
Обучение с градиентным спуском
Итак, у нас есть схема НС – как ей обучиться распознавать цифры? Первое, что нам понадобится – это обучающие данные, т.н. набор обучающих данных. Мы будем использовать
набор MNIST, содержащий десятки тысяч отсканированных изображений рукописных цифр, и их правильную классификацию. Название MNIST получил из-за того, что является изменённым подмножеством двух наборов данных, собранных
NIST, Национальным институтом стандартов и технологий США. Вот несколько изображений из MNIST:

Это те же самые цифры, что были приведены в начале главы как задачка на распознавание. Конечно, при проверке НС мы попросим её распознать не те изображения, которые уже были в обучающем наборе!
Данные MNIST состоят из двух частей. Первая содержит 60 000 изображений, предназначенных для обучения. Это отсканированные рукописные записи 250 человек, половина из которых были сотрудниками Бюро переписи населения США, а вторая половина – старшеклассниками. Изображения чёрно-белые, размером 28х28 пикселей. Вторая часть набора данных MNIST – 10 000 изображений для проверки сети. Это тоже чёрно-белые изображения 28х28 пикселей. Мы будем использовать эти данные, чтобы оценить, насколько хорошо сеть научилась распознавать цифры. Чтобы улучшить качество оценки, эти цифры были взяты у других 250 людей, не участвовавших в записи обучающего набора (хотя это тоже были сотрудники Бюро и старшеклассники). Это помогает нам убедиться в том, что наша система может распознавать рукописный ввод людей, который она не встречала при обучении.
Обучающие входные данные мы обозначим через x. Будет удобно относиться к каждому входному изображению х как к вектору с 28х28=784 измерениями. Каждая величина внутри вектора обозначает яркость одного пикселя изображения. Выходное значение мы будем обозначать, как y=y(x), где у – десятимерный вектор. К примеру, если определённое обучающее изображение х содержит 6, тогда y(x)=(0,0,0,0,0,0,1,0,0,0)
T будет нужным нам вектором. T – операция транспонирования, превращающая вектор-строку в вектор-столбец.
Нам хочется найти алгоритм, позволяющим нам искать такие веса и смещения, чтобы выход сети приближался к y(x) для всех обучающих входных х. Чтобы количественно оценить приближение к этой цели, определим функцию стоимости (иногда называемую
функцией потерь; в книге мы будем использовать функцию стоимости, однако имейте в виду и другое название):
Здесь w обозначает набор весов сети, b – набор смещений, n – количество обучающих входных данных, a – вектор выходных данных, когда х – входные данные, а сумма проходит по всем обучающим входным данным х. Выход, конечно, зависит от x, w и b, но для простоты я не стал обозначать эту зависимость. Обозначение ||v|| означает длину вектора v. Мы будем называть C квадратичной функцией стоимости; иногда её ещё называют среднеквадратичной ошибкой, или MSE. Если присмотреться к C, видно, что она не отрицательна, поскольку все члены суммы неотрицательны. Кроме того, стоимость C(w,b) становится малой, то есть, C(w,b) ≈ 0, именно тогда, когда y(x) примерно равна выходному вектору a у всех обучающих входных данных х. Так что наш алгоритм сработал хорошо, если сумел найти веса и смещения такие, что C(w,b) ≈ 0. И наоборот, сработал плохо, когда C(w,b) большая – это означает, что y(x) не совпадает с выходом для большого количества входных данных. Получается, цель обучающего алгоритма – минимизация стоимости C(w,b) как функции весов и смещений. Иначе говоря, нам нужно найти набор весов и смещений, минимизирующий значение стоимости. Мы будем делать это при помощи алгоритма под названием градиентный спуск.
Зачем нам нужна квадратичная стоимость? Разве нас не интересует в основном количество правильно распознанных сетью изображений? Нельзя ли просто максимизировать это число напрямую, а не минимизировать промежуточное значение квадратичной стоимости? Проблема в том, что количество правильно распознанных изображений не является гладкой функцией весов и смещений сети. По большей части, небольшие изменения весов и смещений не изменят количество правильно распознанных изображений. Из-за этого тяжело понять, как менять веса и смещения для улучшения эффективности. Если же мы будем использовать гладкую функцию стоимости, нам будет легко понять, как вносить небольшие изменения в веса и смещения, чтобы улучшать стоимость. Поэтому мы сначала сконцентрируемся на квадратичной стоимости, а потом уже изучим точность классификации.
Даже учитывая то, что мы хотим использовать гладкую функцию стоимости, вы всё равно можете интересоваться – почему мы выбрали квадратичную функцию для уравнения (6)? Разве её нельзя выбрать произвольно? Возможно, если бы мы выбрали другую функцию, мы бы получили совершенно другой набор минимизирующих весов и смещений? Разумный вопрос, и позднее мы вновь изучим функцию стоимости и внесём в неё некоторые правки. Однако квадратичная функция стоимости прекрасно работает для понимания базовых вещей в обучении НС, поэтому пока мы будем придерживаться её.
Подведём итог: наша цель в обучении НС сводится к поиску весов и смещений, минимизирующих квадратичную функцию стоимости C(w, b). Задача хорошо поставлена, однако пока что у неё есть много отвлекающих структур – интерпретация w и b как весов и смещений, притаившаяся на заднем плане функция σ, выбор архитектуры сети, MNIST и так далее. Оказывается, что мы очень многое можем понять, игнорируя большую часть этой структуры, и концентрируясь только на аспекте минимизации. Так что пока мы забудем об особой форме функции стоимости, связи с НС и так далее. Вместо этого мы собираемся представить, что у нас просто есть функция со многими переменными, и мы хотим её минимизировать. Мы разработаем технологию под названием градиентный спуск, которую можно использовать для решения таких задач. А потом мы вернёмся к определённой функции, которую хотим минимизировать для НС.
Хорошо, допустим, мы пытаемся минимизировать некую функцию C(v). Это может быть любая функция с вещественными значениями от многих переменных v = v
1, v
2,… Заметьте, что я заменил запись w и b на v, чтобы показать, что это может быть любая функция – мы уже не зацикливаемся на НС. Полезно представлять себе, что у функции C есть только две переменных — v
1 и v
2:
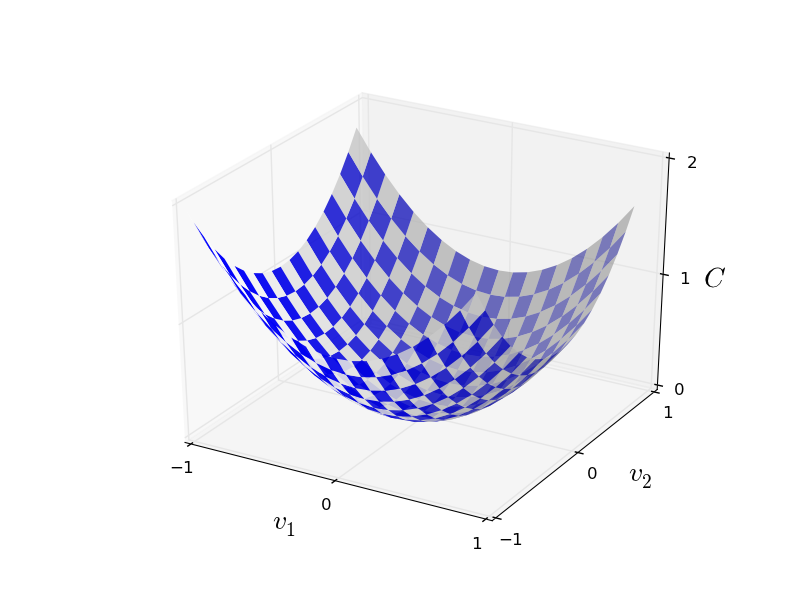
Мы бы хотели найти, где C достигает глобального минимума. Конечно, у нарисованной выше функции мы можем изучить график и найти минимум. В этом смысле я, возможно, дал вам слишком простую функцию! В общем случае C может быть сложной функцией многих переменных, и обычно невозможно просто посмотреть на график и найти минимум.
Один из способов решения задачи – использовать алгебру для поиска минимума аналитическим путём. Мы можем вычислить производные и попытаться использовать их для поиска экстремума. Если нам повезёт, это сработает, когда С будет функцией от одной-двух переменных. Но при большом количестве переменных это превращается в кошмар. А для НС нам часто нужно гораздо больше переменных – у крупнейших НС функции стоимости сложным образом зависят от миллиардов весов и смещений. Использовать алгебру для минимизации этих функций не получится!
(Заявив, что нам будет удобнее считать C функцией двух переменных, я дважды в двух параграфах сказал «да, но что, если это функция гораздо большего количества переменных?». Прошу прощения. Поверьте, что нам и правда будет полезно представлять С как функцию двух переменных. Просто иногда эта картинка разваливается, из-за чего и понадобились два предыдущих параграфа. Для математических рассуждений часто требуется жонглировать несколькими интуитивными представлениями, обучаясь при этом тому, когда представление можно использовать, а когда нельзя.)
Ладно, значит, алгебра не сработает. К счастью, существует прекрасная аналогия, предлагающая хорошо работающий алгоритм. Мы представляем себе нашу функцию чем-то вроде долины. С последним графиком это будет не так сложно сделать. И мы представляем себе шар, катящийся по склону долины. Наш опыт говорит нам, что шар в итоге скатится на самый низ. Возможно, мы можем использовать эту идею для поиска минимума функции? Мы случайным образом выберем начальную точку для воображаемого шара, а потом симулируем движение шара, как будто он скатывается на дно долины. Эту симуляцию мы можем использовать просто подсчитывая производные (и, возможно, вторые производные) С – они скажут нам всё о локальной форме долины, и, следовательно, о том, как наш шарик будет катиться.
На основе написанного вы можете подумать, что мы запишем уравнения движения Ньютона для шара, рассмотрим влияние трения и гравитации, и так далее. На самом деле, мы не будем так уж близко следовать этой аналогии с шаром – мы разрабатываем алгоритм минимизации С, а не точную симуляцию законов физики! Эта аналогия должна стимулировать наше воображение, а не ограничивать мышление. Так что вместо погружения в сложные детали физики, давайте зададим вопрос: если бы нас назначили богом на один день, и мы создавали бы свои законы физики, говоря шару, как ему катиться какой закон или законы движения мы бы выбрали, чтобы шар всегда скатывался на дно долины?
Чтобы уточнить вопрос, подумаем, что произойдёт, если мы передвинем шар на небольшое расстояние Δv
1 в направлении v
1, и на небольшое расстояние Δv
2 в направлении v
2. Алгебра говорит нам, что С меняется следующим образом:
Мы наёдем способ выбора таких Δv
1 и Δv
2, чтобы ΔC была меньше нуля; то есть, мы будем выбирать их так, чтобы шар катился вниз. Чтобы понять, как это сделать, полезно определить Δv как вектор изменений, то есть Δv ≡ (Δv
1, Δv
2)
T, где Т – операция транспонирования, превращающая вектора-строки в вектора-столбцы. Мы также определим градиент С как вектор частных производных (∂С/ ∂v
1, ∂С/∂v
2)
T. Обозначать градиентный вектор мы будем ∇С:
Скоро мы перепишем изменение ΔC через Δv и градиент ∇C. А пока я хочу прояснить кое-что, из-за чего люди часто подвисают на градиенте. Впервые встретившись с записью ∇C, люди иногда не понимают, как они должны воспринимать символ ∇. Что он конкретно означает? На самом деле можно спокойно считать ∇С единым математическим объектом – определённым ранее вектором – который просто записывается с использованием двух символов. С этой точки зрения, ∇ — это как размахивать флагом, сообщающим о том, что "∇С – это градиентный вектор". Существуют и более продвинутые точки зрения, с которых ∇ можно рассматривать, как независимую математическую сущность (к примеру, как оператор дифференцирования), однако нам они не понадобятся.
С такими определениями выражение (7) можно переписать, как:
Это уравнение помогает объяснить, почему ∇C называют градиентным вектором: он связывает изменения в v с изменениями С, именно так, как и ожидается от сущности под названием градиент. [англ. gradient – отклонение / прим. перев.] Однако более интересно, что это уравнение позволяет нам увидеть, как выбрать Δv так, чтобы ΔC было отрицательным. Допустим, мы выберем
где η — небольшой положительный параметр (скорость обучения). Тогда уравнение (9) говорит нам о том, что ΔC ≈ — η ∇C ċ = — η ||∇C||
2. Поскольку ||∇C||
2 ≥ 0, это гарантирует, что ΔC ≤ 0, то есть С будет всё время уменьшаться, если мы будем менять v, как прописано в (10) (конечно, в рамках аппроксимации из уравнения (9)). А именно это нам и надо! Поэтому мы возьмём уравнение (10) для определения «закона движения» шара в нашем алгоритме градиентного спуска. То есть, мы будем использовать уравнение (10) для вычисления значения Δv, а потом будем двигать шар на это значение:
Потом мы снова применим это правило, для следующего хода. Продолжая повторение, мы будем понижать С, пока, как мы надеемся, не достигнем глобального минимума.
Подытоживая, градиентный спуск работает через последовательное вычисление градиента ∇ C, и последующее смещение в противоположном направлении, что приводит к «падению» по склону долины. Визуализировать это можно так:
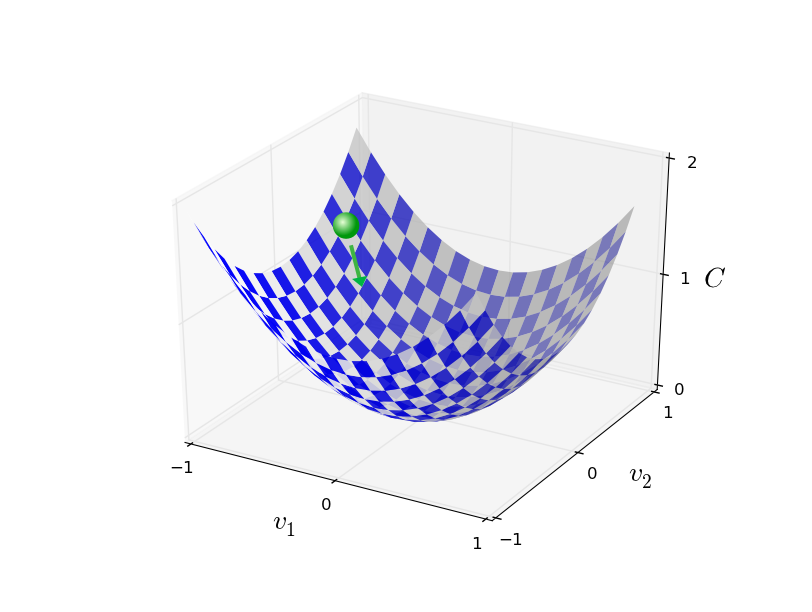
Отметьте, что с этим правилом градиентный спуск не воспроизводит реального физического движения. В реальной жизни у шара есть импульс, который может позволить ему катиться поперёк уклона, или даже какое-то время катиться вверх. Только после работы силы трения шар гарантированно скатится вниз долины. Наше же правило выбора Δv просто говорит «иди вниз». Достаточно неплохое правило для нахождения минимума!
Чтобы градиентный спуск работал правильно, нам нужно выбрать достаточно малое значение скорости обучения η, чтобы уравнение (9) было хорошей аппроксимацией. В противном случае может получиться, что ΔC > 0 – ничего хорошего! В то же время, не нужно, чтобы η была слишком маленькой, поскольку тогда изменения Δv будут крохотными, и алгоритм будет работать слишком медленно. На практике η меняется так, чтобы уравнение (9) давало неплохую аппроксимацию, и при этом алгоритм работал не слишком медленно. Позднее мы увидим, как это работает.
Я объяснял градиентный спуск, когда функция С зависела только от двух переменных. Но всё работает так же, если С будет функцией от многих переменных. Допустим, что у неё есть m переменных, v
1,…, v
m. Тогда изменение ΔC, вызванное небольшим изменением Δv = (Δv
1,…, Δv
m)
T будет равняться
где градиент ∇C – это вектор
Как и в случае с двумя переменными, мы можем выбрать
и гарантировать, что наше приблизительное выражение (12) для ΔC будет отрицательным. Это даёт нам способ идти по градиенту до минимума, даже когда С будет функцией многих переменных, раз за разом применяя правило обновления
Это правило обновления можно считать определяющим алгоритм градиентного спуска. Оно даёт нам метод неоднократного изменения положения v в поисках минимума функции С. Это правило работает не всегда – несколько вещей может пойти не так, помешав градиентному спуску найти глобальный минимум С – к этому моменту мы вернёмся в следующих главах. Но на практике градиентный спуск часто работает очень хорошо, и мы увидим, что в НС это действенный способ минимизации функции стоимости, и, следовательно, обучения сети.
В каком-то смысле градиентный спуск можно считать оптимальной стратегией поиска минимума. Допустим, что мы пытаемся сдвинуться на Δv в позицию для максимального уменьшения С. Это эквивалентно минимизации ΔC ≈ ∇C ċ Δv. Мы ограничим размер шага так, чтобы ||Δv|| = ε для некоего малого постоянного ε > 0. Иначе говоря, мы хотим сдвинуться на небольшое расстояние фиксированного размера, и пытаемся найти направление движение, уменьшающее С так сильно, как это возможно. Можно доказать, что выбор Δv, минимизирующий ∇C ċ Δv, равняется Δv = -η∇C, где η = ε/||∇C||, определяется ограничением ||Δv|| = ε. Так что градиентный спуск можно считать способом делать небольшие шаги в направлении, наиболее сильно уменьшающем С.
Упражнения
- Докажите утверждение из последнего параграфа. Подсказка: если вы не знакомы с неравенством Коши — Буняковского, возможно, вам поможет, если вы узнаете о нём побольше.
- Я объяснял про градиентный спуск, когда С является функцией двух переменных, и когда она является функцией многих переменных. Что будет, если С будет функцией всего одной переменной? Можете ли вы дать геометрическую интерпретацию работы градиентного спуска в одномерном случае?
Люди изучили множество вариантов градиентного спуска, включая и те, что более точно воспроизводят реальный физический шар. У таких вариантов есть свои преимущества, но и большой недостаток: необходимость вычисления вторых частных производных С, что может отнимать много ресурсов. Чтобы понять это, допустим, что нам надо вычислить все вторые частные производные ∂
2C / ∂v
j∂v
k. Если переменных v
j миллион, тогда нам нужно вычислить примерно триллион (миллион в квадрате) вторых частных производных (на самом деле, полтриллиона, поскольку ∂
2C / ∂v
j∂v
k = ∂
2C / ∂v
k∂v
j. Но суть вы уловили). Это потребует много вычислительных ресурсов. Есть трюки, помогающие избежать этого, и поиск альтернатив градиентного спуска является областью активных исследований. Однако в этой книге мы будем использовать градиентный спуск и его варианты в качестве основного подхода к обучению НС.
Как нам применить градиентный спуск к обучению НС? Нам нужно использовать его для поиска весов w
k и смещений b
l, минимизирующих уравнение стоимости (6). Давайте перезапишем правило обновления градиентного спуска, заменив переменные v
j весами и смещениями. Иначе говоря, теперь у нашей «позиции» есть компоненты w
k и b
l, а у градиентного вектора ∇C есть соответствующие компоненты ∂C/∂w
k и ∂C/∂b
l. Записав наше правило обновления с новыми компонентами, мы получим:
Повторно применяя это правило обновления, мы можем «катиться под горку», и, если повезёт, найти минимум функции стоимости. Иначе говоря, это правило можно использовать для обучения НС.
Применению правила градиентного спуска есть несколько препятствий. Подробнее мы изучим их в следующих главах. Но пока я хочу упомянуть только одну проблему. Чтобы понять её, давайте вернёмся к квадратичной стоимости в уравнении (6). Заметьте, что эта функция стоимости выглядит, как C = 1/n ∑
x C
x, то есть это среднее по стоимости C
x ≡ (||y(x)−a||
2)/2 для отдельных обучающих примеров. На практике для вычисления градиента ∇C нам нужно вычислять градиенты ∇C
x отдельно для каждого обучающего входа x, а потом усреднять их, ∇C = 1/n ∑
x ∇C
x. К сожалению, когда количество входных данных будет очень большим, это займёт очень много времени, и такое обучение будет проходить медленно.
Для ускорения обучения можно использовать стохастический градиентный спуск. Идея в том, чтобы приблизительно вычислить градиент ∇C, вычислив ∇C
x для небольшой случайной выборки обучающих входных данных. Посчитав их среднее, мы можем быстро получить хорошую оценку истинного градиента ∇C, и это помогает ускорить градиентный спуск, и, следовательно, обучение.
Формулируя более точно, стохастический градиентный спуск работает через случайную выборку небольшого количества m обучающих входных данных. Мы назовём эти случайные данные X
1, X
2,.., X
m, и назовём их мини-пакетом. Если размер выборки m будет достаточно большим, среднее значение ∇C
Xj будет достаточно близким к среднему по всем ∇Cx, то есть
где вторая сумма идёт по всему набору обучающих данных. Поменяв части местами, мы получим
что подтверждает, что мы можем оценить общий градиент, вычислив градиенты для случайно выбранного мини-пакета.
Чтобы связать это непосредственно с обучением НС, допустим, что w
k и b
l обозначают веса и смещения нашей НС. Тогда стохастический градиентный спуск выбирает случайный мини-пакет входных данных, и обучается на них
где идёт суммирование по всем обучающим примерам X
j в текущем мини-пакете. Затем мы выбираем ещё один случайный мини-пакет и обучаемся на нём. И так далее, пока мы не исчерпаем все обучающие данные, что называется окончанием обучающей эпохи. В этот момент мы начинаем заново новую эпоху обучения.
Кстати, стоит отметить, что соглашения по поводу масштабирования функции стоимости и обновлений весов и смещений мини-пакетом разнятся. В уравнении (6) мы масштабировали функцию стоимости в 1/n раз. Иногда люди опускают 1/n, суммируя стоимости отдельных обучающих примеров, вместо вычисления среднего. Это полезно, когда общее количество обучающих примеров заранее неизвестно. Такое может случиться, например, когда дополнительные данные появляются в реальном времени. Таким же образом правила обновления мини-пакета (20) и (21) иногда опускают член 1/m перед суммой. Концептуально это ни на что не влияет, поскольку это эквивалентно изменению скорости обучения η. Однако на это стоит обращать внимание при сравнении различных работ.
Стохастический градиентный спуск можно представлять себе, как политическое голосование: гораздо проще взять выборку в виде мини-пакета, чем применить градиентный спуск к полной выборке – точно так же, как опрос на выходе из участка провести проще, чем провести полноценные выборы. К примеру, если наш обучающий набор имеет размер n = 60 000, как MNIST, и мы сделаем выборку мини-пакета размером m = 10, то в 6000 раз ускорит оценку градиента! Конечно, оценка не будет идеальной – в ней будет статистическая флуктуация – но ей и не надо быть идеальной: нам лишь надо двигаться в примерно том направлении, которое уменьшает С, а это значит, что нам не нужно точно вычислять градиент. На практике стохастический градиентный спуск – распространённая и мощная техника обучения НС, и база большинства обучающих технологий, которые мы разработаем в рамках книги.
Упражнения
- Экстремальная версия градиентного спуска использует размер мини-пакета равный 1. То есть, при входных данных x мы обновляем наши веса и смещения по правилам wk → w′ k = wk − η ∂Cx / ∂wk и bl → b′l = bl − η ∂Cx / ∂bl. Затем мы выбираем другой пример обучающих входных данных и снова обновляем веса и смещения. И так далее. Эта процедура известна, как онлайн-, или инкрементальное обучение. В онлайн-обучении НС учиться на основе одного обучающего экземпляра входных данных за раз (как люди). Назовите одно преимущество и один недостаток онлайн-обучения по сравнению со стохастическим градиентным спуском с размером мини-пакета в 20.
Позвольте закончить этот раздел обсуждением темы, которая иногда беспокоит людей, впервые столкнувшихся с градиентным спуском. У НС стоимость С является функцией многих переменных – всех весов и смещений – и в каком-то смысле, определяет поверхность в очень многомерном пространстве. Люди начинают думать: «Мне придётся визуализировать все эти дополнительные измерения». И начинают волноваться: «Я не могу ориентироваться в четырёх измерениях, не говоря уже о пяти (или пяти миллионах)». Не отсутствует ли у них какое-то особое качество, имеющееся у «настоящих» сверхматематиков? Конечно же, нет. Даже профессиональные математики не могут визуализировать четырёхмерное пространство достаточно хорошо – если вообще могут. Они идут на хитрости, вырабатывая иные способы представления происходящего. Мы именно это и сделали: мы использовали алгебраическое (а не визуальное) представление ΔC, чтобы понять, как нужно двигаться, чтобы С уменьшалась. У людей, хорошо справляющихся с большим числом измерений, в уме находится большая библиотека подобных техник; наш алгебраический трюк – всего лишь один из примеров. Эти техники, возможно, не такие простые, к каким привыкли мы при визуализации трёх измерений, но когда вы создали библиотеку подобных техник, вы начинаете неплохо мыслить в высших измерениях. Не буду углубляться в детали, но если вам это интересно, вам может понравиться
обсуждение некоторых из этих техник профессиональными математиками, привыкшими мыслить в высших измерениях. И хотя некоторые из обсуждаемых техник весьма сложны, большая часть лучших ответов интуитивны и доступны для всех.
Реализация сети для классификации цифр
Хорошо, теперь давайте напишем программу, обучающуюся распознаванию рукописных цифр с использованием стохастического градиентного спуска и обучающих данных от MNIST. Мы сделаем это при помощи короткой программы на python 2.7, состоящей всего из 74 строк! Первое, что нам нужно – скачать данные MNIST. Если вы используете git, тогда их можно получить, клонировав репозиторий этой книги:
git clone https://github.com/mnielsen/neural-networks-and-deep-learning.git
Если нет, скачайте код
по ссылке.
Кстати, когда раньше я упоминал данные MNIST, я сказал, что они разбиты на 60 000 обучающих изображений и 10 000 проверочных. Таково официальное описание от MNIST. Мы же разобьём данные немного по-другому. Мы оставим проверочные изображения без изменений, но разобьём обучающий набор на две части: 50 000 картинок, которые мы будем использовать для обучения НС, и отдельные 10 000 картинок для дополнительной ратификации. Пока мы их не будем использовать, но позже они будут полезны нам, когда мы будем разбираться в настройке некоторых гиперпараметров НС – скорости обучения, и т.д., — которые наш алгоритм не выбирает напрямую. Хотя ратификационные данные не входят в изначальную спецификацию MNIST, многие используют MNIST именно так, и в области НС использование ратификационных данных встречается часто. Теперь, говоря об «обучающих данных MNIST», я буду иметь в виду наши 50 000 каритнок, а не изначальные 60 000.
Кроме данных MNIST нам для быстрых вычислений линейной алгебры также понадобится библиотека для python под названием
Numpy. Если её у вас нет, вы можете взять её
по ссылке.
Перед тем, как выдать вам всю программу, позвольте объяснить основные особенности кода для НС. Центральное место занимает класс Network, который мы используем для представления НС. Вот код инициализации объекта Network:
class Network(object):
def __init__(self, sizes):
self.num_layers = len(sizes)
self.sizes = sizes
self.biases = [np.random.randn(y, 1) for y in sizes[1:]]
self.weights = [np.random.randn(y, x)
for x, y in zip(sizes[:-1], sizes[1:])]
Массив sizes содержит количество нейронов в соответствующих слоях. Так что, если мы хотим создать объект Network с двумя нейронами в первом слое, тремя нейронами во втором слое, и одним нейроном в третьем, то мы запишем это так:
net = Network([2, 3, 1])
Смещения и веса в объекте Network инициализируются случайным образом с использованием функции np.random.randn из Numpy, которая генерирует распределение Гаусса с математическим ожиданием 0 и среднеквадратичным отклонением 1. Такая случайная инициализация даёт нашему алгоритму стохастического градиентного спуска отправную точку. В следующих главах мы найдём лучшие способы инициализации весов и смещений, но пока хватит и этого. Отметьте, что код инициализации Network предполагает, что первый слой нейронов будет входным, и не назначает им смещения, поскольку они используются только при подсчёте выходных данных.
Также отметьте, что смещения и веса хранятся как массив матриц Numpy. К примеру, net.weights[1] – матрица Numpy, хранящая веса, соединяющие второй и третий слои нейронов (это не первый и второй слои, поскольку в python нумерация элементов массива идет с нуля). Поскольку писать net.weights[1] будет слишком долго, обозначим эту матрицу, как w. Это такая матрица, что w
jk — это вес связи между k-м нейроном во втором слое и j-м нейроном в третьем. Такой порядок индексов j и k может показаться странным — не было бы логичнее поменять их местами? Но большим преимуществом такой записи будет то, что вектор активаций третьего слоя нейронов получается:
Давайте разберём это довольно насыщенное уравнение. a – вектор активаций второго слоя нейронов. Чтобы получить a', мы умножаем a на матрицу весов w, и добавляем вектор смещений b. Затем мы применяем сигмоиду σ поэлементно к каждому элементу вектора wa+b (это называется векторизацией функции σ). Легко проверить, что уравнение (22) даёт такой же результат, что и правило (4) для вычисления сигмоидного нейрона.
Упражнение
- Запишите уравнение (22) в компонентной форме, и убедитесь, что оно даёт тот же результат, что и правило (4) для вычисления сигмоидного нейрона.
Учитывая всё это, легко написать код, вычисляющий выходные данные объекта Network. Мы начнём с определения сигмоиды:
def sigmoid(z):
return 1.0/(1.0+np.exp(-z))
Учтите, что когда параметр z будет вектором или массивом Numpy, то Numpy автоматически будет применять сигмоиду поэлементно, то есть, в векторном виде.
Добавим метод прямого распространения в класс Network, который принимает на вход a от сети и возвращает соответствующие выходные данные. Предполагается, что параметр a – это (n, 1) Numpy ndarray, а не вектор (n,). Здесь n – количество входных нейронов. Если вы попытаетесь использовать вектор (n,), то получите странные результаты.
Метод просто применяет уравнение (22) к каждому слою:
def feedforward(self, a):
"""Вернуть выходные данные сети при входных данных "a""""
for b, w in zip(self.biases, self.weights):
a = sigmoid(np.dot(w, a)+b)
return a
Конечно, в основном нам от объектов Network нужно, чтобы они обучались. Для этого мы дадим им метод SGD, реализующий стохастический градиентный спуск. Вот его код. В некоторых местах он довольно загадочный, но ниже мы разберём его подробнее.
def SGD(self, training_data, epochs, mini_batch_size, eta,
test_data=None):
"""Обучаем сеть при помощи мини-пакетов и стохастического градиентного спуска. training_data – список кортежей "(x, y)", обозначающих обучающие входные данные и желаемые выходные. Остальные обязательные параметры говорят сами за себя. Если test_data задан, тогда сеть будет оцениваться относительно проверочных данных после каждой эпохи, и будет выводиться текущий прогресс. Это полезно для отслеживания прогресса, однако существенно замедляет работу. """
if test_data: n_test = len(test_data)
n = len(training_data)
for j in xrange(epochs):
random.shuffle(training_data)
mini_batches = [
training_data[k:k+mini_batch_size]
for k in xrange(0, n, mini_batch_size)]
for mini_batch in mini_batches:
self.update_mini_batch(mini_batch, eta)
if test_data:
print "Epoch {0}: {1} / {2}".format(
j, self.evaluate(test_data), n_test)
else:
print "Epoch {0} complete".format(j)
training_data – список кортежей "(x, y)", обозначающих обучающие входные данные и желаемые выходные. Переменные epochs и mini_batch_size – это количество эпох для обучения и размер мини-пакетов для использования. eta – скорость обучения, η. Если test_data задан, тогда сеть будет оцениваться относительно проверочных данных после каждой эпохи, и будет выводиться текущий прогресс. Это полезно для отслеживания прогресса, однако существенно замедляет работу.
Код работает так. В каждую эпоху он начинает с того, что случайно перемешивает обучающие данные, а потом разбивает их на мини-пакеты нужного размера. Это простой способ создания выборки из обучающих данных. Затем для каждого mini_batch мы применяем один шаг градиентного спуска. Это делает код self.update_mini_batch(mini_batch, eta), обновляющий веса и смещения сети в соответствии с одной итерацией градиентного спуска, используя только обучающие данные в mini_batch. Вот код для метода update_mini_batch:
def update_mini_batch(self, mini_batch, eta):
"""Обновить веса и смещения сети, применяя градиентный спуск с использованием обратного распространения к одному мини-пакету. mini_batch – это список кортежей (x, y), а eta – скорость обучения."""
nabla_b = [np.zeros(b.shape) for b in self.biases]
nabla_w = [np.zeros(w.shape) for w in self.weights]
for x, y in mini_batch:
delta_nabla_b, delta_nabla_w = self.backprop(x, y)
nabla_b = [nb+dnb for nb, dnb in zip(nabla_b, delta_nabla_b)]
nabla_w = [nw+dnw for nw, dnw in zip(nabla_w, delta_nabla_w)]
self.weights = [w-(eta/len(mini_batch))*nw
for w, nw in zip(self.weights, nabla_w)]
self.biases = [b-(eta/len(mini_batch))*nb
for b, nb in zip(self.biases, nabla_b)]
Большую часть работы делает строчка
delta_nabla_b, delta_nabla_w = self.backprop(x, y)
Она вызывает алгоритм обратного распространения – это быстрый способ вычислить градиент функции стоимости. Так что update_mini_batch просто вычисляет эти градиенты для каждого обучающего примера из mini_batch, а потом обновляет self.weights и self.biases.
Пока что я не будут демонстрировать код для self.backprop. Работу обратного распространения мы изучим в следующей главе, и там будет код self.backprop. Пока что предположим, что он ведёт себя, как заявлено, возвращая соответствующий градиент для стоимости, связанной с обучающим примером х.
Давайте посмотрим на программу целиком, включая поясняющие комментарии. За исключением функции self.backprop программа говорит сама за себя – основную работу проделывают self.SGD и self.update_mini_batch. Метод self.backprop использует несколько дополнительных функций для вычисления градиента, а именно, sigmoid_prime, вычисляющую производную сигмоиды, и self.cost_derivative, которую я не буду описывать здесь. Вы можете получить о них представление, изучив код и комментарии. В следующей главе мы рассмотрим их подробнее. Учтите, что, хотя программа кажется длинной, большая часть кода – это комментарии, облегчающие понимание. На самом деле сама программа состоит всего из 74 не строк кода – не пустых и не комментариев. Весь
код доступен на GitHub.
"""
network.py
~~~~~~~~~~
Модуль реализации обучающего алгоритма стохастического градиентного спуска для нейросети прямого распространения. Градиенты вычисляются при помощи обратного распространения. Я специально делал код простым, читаемым и легко модифицируемым. Он не оптимизирован, и в нём нет многих желательных вещей.
"""
#### Библиотеки
# Стандартная библиотека
import random
# Сторонние библиотеки
import numpy as np
class Network(object):
def __init__(self, sizes):
""" Массив sizes содержит количество нейронов в соответствующих слоях. Так что, если мы хотим создать объект Network с двумя нейронами в первом слое, тремя нейронами во втором слое, и одним нейроном в третьем, то мы запишем это, как [2, 3, 1]. Смещения и веса сети инициализируются случайным образом с использованием распределения Гаусса с математическим ожиданием 0 и среднеквадратичным отклонением 1. Предполагается, что первый слой нейронов будет входным, и поэтому у его нейронов нет смещений, поскольку они используются только при подсчёте выходных данных. """
self.num_layers = len(sizes)
self.sizes = sizes
self.biases = [np.random.randn(y, 1) for y in sizes[1:]]
self.weights = [np.random.randn(y, x)
for x, y in zip(sizes[:-1], sizes[1:])]
def feedforward(self, a):
"""Возвращает выходные данные сети, когда ``a`` - входные данные."""
for b, w in zip(self.biases, self.weights):
a = sigmoid(np.dot(w, a)+b)
return a
def SGD(self, training_data, epochs, mini_batch_size, eta,
test_data=None):
"""Обучаем сеть при помощи мини-пакетов и стохастического градиентного спуска. training_data – список кортежей "(x, y)", обозначающих обучающие входные данные и желаемые выходные. Остальные обязательные параметры говорят сами за себя. Если test_data задан, тогда сеть будет оцениваться относительно проверочных данных после каждой эпохи, и будет выводиться текущий прогресс. Это полезно для отслеживания прогресса, однако существенно замедляет работу. """
if test_data: n_test = len(test_data)
n = len(training_data)
for j in xrange(epochs):
random.shuffle(training_data)
mini_batches = [
training_data[k:k+mini_batch_size]
for k in xrange(0, n, mini_batch_size)]
for mini_batch in mini_batches:
self.update_mini_batch(mini_batch, eta)
if test_data:
print "Epoch {0}: {1} / {2}".format(
j, self.evaluate(test_data), n_test)
else:
print "Epoch {0} complete".format(j)
def update_mini_batch(self, mini_batch, eta):
"""Обновить веса и смещения сети, применяя градиентный спуск с использованием обратного распространения к одному мини-пакету. mini_batch – это список кортежей (x, y), а eta – скорость обучения."""
nabla_b = [np.zeros(b.shape) for b in self.biases]
nabla_w = [np.zeros(w.shape) for w in self.weights]
for x, y in mini_batch:
delta_nabla_b, delta_nabla_w = self.backprop(x, y)
nabla_b = [nb+dnb for nb, dnb in zip(nabla_b, delta_nabla_b)]
nabla_w = [nw+dnw for nw, dnw in zip(nabla_w, delta_nabla_w)]
self.weights = [w-(eta/len(mini_batch))*nw
for w, nw in zip(self.weights, nabla_w)]
self.biases = [b-(eta/len(mini_batch))*nb
for b, nb in zip(self.biases, nabla_b)]
def backprop(self, x, y):
"""Вернуть кортеж ``(nabla_b, nabla_w)``, представляющий градиент для функции стоимости C_x. ``nabla_b`` и ``nabla_w`` - послойные списки массивов numpy, похожие на ``self.biases`` and ``self.weights``."""
nabla_b = [np.zeros(b.shape) for b in self.biases]
nabla_w = [np.zeros(w.shape) for w in self.weights]
# прямой проход
activation = x
activations = [x] # список для послойного хранения активаций
zs = [] # список для послойного хранения z-векторов
for b, w in zip(self.biases, self.weights):
z = np.dot(w, activation)+b
zs.append(z)
activation = sigmoid(z)
activations.append(activation)
# обратный проход
delta = self.cost_derivative(activations[-1], y) * \
sigmoid_prime(zs[-1])
nabla_b[-1] = delta
nabla_w[-1] = np.dot(delta, activations[-2].transpose())
"""Переменная l в цикле ниже используется не так, как описано во второй главе книги. l = 1 означает последний слой нейронов, l = 2 – предпоследний, и так далее. Мы пользуемся преимуществом того, что в python можно использовать отрицательные индексы в массивах."""
for l in xrange(2, self.num_layers):
z = zs[-l]
sp = sigmoid_prime(z)
delta = np.dot(self.weights[-l+1].transpose(), delta) * sp
nabla_b[-l] = delta
nabla_w[-l] = np.dot(delta, activations[-l-1].transpose())
return (nabla_b, nabla_w)
def evaluate(self, test_data):
"""Вернуть количество проверочных входных данных, для которых нейросеть выдаёт правильный результат. Выходные данные сети – это номер нейрона в последнем слое с наивысшим уровнем активации."""
test_results = [(np.argmax(self.feedforward(x)), y)
for (x, y) in test_data]
return sum(int(x == y) for (x, y) in test_results)
def cost_derivative(self, output_activations, y):
"""Вернуть вектор частных производных (чп C_x / чп a) для выходных активаций."""
return (output_activations-y)
#### Разные функции
def sigmoid(z):
"""Сигмоида."""
return 1.0/(1.0+np.exp(-z))
def sigmoid_prime(z):
"""Производная сигмоиды."""
return sigmoid(z)*(1-sigmoid(z))
Насколько хорошо программа распознаёт рукописные цифры? Начнём с загрузки данных MNIST. Сделаем это при помощи небольшой вспомогательной программы mnist_loader.py, которую я опишу ниже. Выполним следующие команды в оболочке python:
>>> import mnist_loader
>>> training_data, validation_data, test_data = \
... mnist_loader.load_data_wrapper()
Это, конечно, можно сделать в отдельной программе, но если вы работаете параллельно с книгой, так будет проще.
После загрузки данных MNIST настроим сеть из 30 скрытых нейронов. Это мы сделаем после импорта описанной выше программы, которая называется network:
>>> import network
>>> net = network.Network([784, 30, 10])
Наконец, используем стохастический градиентный спуск для обучения на обучающих данных в течение 30 эпох, с размером мини-пакета в 10, и скоростью обучения η=3.0:
>>> net.SGD(training_data, 30, 10, 3.0, test_data=test_data)
Если вы выполняете код параллельно с чтением книги, учтите, что на его выполнение уйдёт несколько минут. Предлагаю вам всё запустить, продолжить чтение, и периодически проверять, что выдаёт программа. Если вы торопитесь, то можете уменьшить количество эпох, уменьшив количество скрытых нейронов, или используя только часть обучающих данных. Окончательный рабочий код будет работать быстрее: данные скрипты на python предназначены для того, чтобы вы поняли, как работает сеть, и не являются высокопроизводительными! И, конечно, после тренировки сеть может работать очень быстро почти на любой вычислительной платформе. К примеру, когда мы обучим сеть хорошему нбаору весов и смещений, её легко можно портировать для работы на JavaScript в веб-браузере, или в качестве нативного приложения на мобильном устройстве. В любом случае, примерно такой вывод даёт программа, обучающая нейросеть. Она пишет количество правильно распознанных проверочных изображений после каждой эпохи тренировок. Как видите, даже после одной эпохи она достигает точности в 9 129 из 10 000, и это число продолжает расти:
Epoch 0: 9129 / 10000
Epoch 1: 9295 / 10000
Epoch 2: 9348 / 10000
...
Epoch 27: 9528 / 10000
Epoch 28: 9542 / 10000
Epoch 29: 9534 / 10000
Получается, что обученная сеть даёт процент правильной классификации около 95 – 95,42% на максимуме! Довольно многообещающая первая попытка. Предупреждаю, что у вас код не обязательно будет выдавать точно такие же результаты, поскольку мы инициализируем сеть случайными весами и смещениями. Для этой главы я выбрал лучшую из трёх попыток.
Давайте-ка перезапустим эксперимент, изменив количество скрытых нейронов до 100. Как и раньше, если вы запускаете код одновременно с чтением, учтите, что его выполнение занимает довольно много времени (на моей машине каждая эпоха занимает несколько десятков секунд), поэтому лучше читать параллельно с исполнением кода.
>>> net = network.Network([784, 100, 10])
>>> net.SGD(training_data, 30, 10, 3.0, test_data=test_data)
Естественно, это улучшает результат до 96,59%. По крайней мере, в этом случае использование большего количества скрытых нейронов помогает получать лучшие результаты.
Отзывы от читателей говорят о том, что результаты данного эксперимента сильно варьируются, и некоторые итоги обучения получаются гораздо хуже. Используя техники из 3-й главы серьёзно уменьшить разнообразие эффективности работы от одного прогона к другому.
Конечно, чтобы достичь такой точности, мне нужно было выбирать определённое количество эпох для обучения, размер мини-пакета и скорость обучения η. Как я упоминал выше, их называют гиперпараметрами нашей НС – чтобы отличать их от простых параметров (весов и смещений), которые алгоритм настраивает в процессе обучения. Если мы плохо выберем гиперпараметры, мы получим плохие результаты. Допустим, к примеру, что мы выбрали скорость обучения η = 0,001:
>>> net = network.Network([784, 100, 10])
>>> net.SGD(training_data, 30, 10, 0.001, test_data=test_data)
Результаты получатся куда как менее впечатляющими:
Epoch 0: 1139 / 10000
Epoch 1: 1136 / 10000
Epoch 2: 1135 / 10000
...
Epoch 27: 2101 / 10000
Epoch 28: 2123 / 10000
Epoch 29: 2142 / 10000
Однако можно видеть, что эффективность сети со временем медленно растёт. Это говорит о том, что можно попробовать увеличить скорость обучения, допустим, до 0,01. В этом случае результаты будут лучше, что говорит о необходимости ещё больше увеличить скорость (если изменение улучшает ситуацию, изменяйте дальше!). Если сделать это несколько раз, мы в итоге придём к η = 1,0 (а иногда даже и 3,0), что близко к нашим более ранним экспериментам. Так что, хотя мы изначально плохо выбрали гиперпараметры, по крайней мере, мы собрали достаточно информации, чтобы суметь улучшить наш выбор параметров.
В целом, отладка НС – дело сложное. Особенно это так, когда выбор изначальных гиперпараметров выдаёт результаты, не превышающие случайного шума. Допустим, мы попробуем использовать успешную архитектуру из 30 нейронов, однако поменяем скорость обучения на 100,0:
>>> net = network.Network([784, 30, 10])
>>> net.SGD(training_data, 30, 10, 100.0, test_data=test_data)
В итоге окажется, что мы зашли слишком далеко, и взяли слишком большую скорость:
Epoch 0: 1009 / 10000
Epoch 1: 1009 / 10000
Epoch 2: 1009 / 10000
Epoch 3: 1009 / 10000
...
Epoch 27: 982 / 10000
Epoch 28: 982 / 10000
Epoch 29: 982 / 10000
Теперь представьте, что мы подходим к этой задаче в первый раз. Конечно, мы знаем из ранних экспериментов, что правильно будет уменьшить скорость обучения. Но если бы мы подступались к этой задаче впервые, у нас не было бы выходных данных, способных привести нас к верному решению. Мы могли бы начать думать о том, что, возможно, мы выбрали неправильные начальные параметры для весов и смещений, и сети трудно обучаться? Или, возможно, у нас недостаточно обучающих данных, чтобы получить осмысленный результат? Возможно, мы не подождали достаточно эпох? Возможно, нейросеть с такой архитектурой просто не может научиться распознавать рукописные цифры? Возможно, скорость обучения слишком мала? При первом подходе к задаче у вас никогда нет уверенности.
Из этого стоит вынести урок о том, что отладка НС не является тривиальной задачей, и это, как и обычное программирование, частью искусство. Вы должны обучиться этому искусству отладки, чтобы получать хорошие результаты от НС. В целом, нам необходимо выработать эвристику для выбора хороших гиперпараметров и хорошей архитектуры. Мы будем подробно обсуждать это в книге, включая то, как я выбрал указанные выше гиперпараметры.
Упражнение
- Попробуйте создать сеть всего из двух слоёв – входного и выходного, без скрытого – с 784 и 10 нейронами соответственно. Обучите сеть при помощи стохастического градиентного спуска. Какую точность классификации вы получите?
Ранее я пропустил детали загрузки данных MNIST. Она происходит довольно просто. Вот код для полноты картины. Структуры данных описаны в комментариях – всё просто, кортежи и массивы объектов Numpy ndarray (если вам не знакомы такие объекты, представляйте их себе как вектора).
"""
mnist_loader
~~~~~~~~~~~~
Библиотека загрузки изображений из базы MNIST. Детали структур описаны в комментариях к ``load_data`` и ``load_data_wrapper``. На практике, ``load_data_wrapper`` - это функция, которую обычно вызывает код НС.
"""
#### Библиотеки
# Стандартные
import cPickle
import gzip
# Сторонние
import numpy as np
def load_data():
"""Вернуть данные MNIST в виде кортежа, содержащего обучающие, ратификационные и проверочные данные. ``training_data`` возвращается как кортеж с двумя вхождениями.
Первое содержит сами картинки. Это numpy ndarray с 50 000 элементами. Каждый элемент – это в свою очередь numpy ndarray с 784 значениями, представляющими 28 * 28 = 784 пикселя одного изображения MNIST.
Второе – это numpy ndarray с 50 000 элементами. Эти элементы – цифры от 0 до 9 для соответствующих изображений, содержащихся в первом вхождении.
``validation_data`` и ``test_data`` похожи, только содержат по 10 000 изображений.
Это удобный формат данных, но для использования в НС полезно будет немного изменить формат ``training_data``. Это делается в функции-обёртке ``load_data_wrapper()``.
"""
f = gzip.open('../data/mnist.pkl.gz', 'rb')
training_data, validation_data, test_data = cPickle.load(f)
f.close()
return (training_data, validation_data, test_data)
def load_data_wrapper():
"""Вернуть кортеж, содержащий ``(training_data, validation_data, test_data)``. На основе ``load_data``, но формат удобнее для использования в нашей реализации НС.
В частности, ``training_data`` - это список из 50 000 кортежей из двух переменных, ``(x, y)``. ``x`` - это 784-размерный numpy.ndarray, содержащий входящее изображение. ``y`` - это 10-мерный numpy.ndarray, представляющий единичный вектор, соответствующий правильной цифре для ``x``.
``validation_data`` и ``test_data`` - это списки, содержащие по 10 000 кортежей из двух переменных, ``(x, y)``. ``x`` - это 784-размерный numpy.ndarray, содержащий входящее изображение, а ``y`` - это соответствующая классификация, то есть, цифровые значения (целые числа), соответствующие ``x``.
Очевидно, это означает, что для тренировочных и ратификационных данных мы используем немного разные форматы. Они оказываются наиболее удобными для использования в коде НС."""
tr_d, va_d, te_d = load_data()
training_inputs = [np.reshape(x, (784, 1)) for x in tr_d[0]]
training_results = [vectorized_result(y) for y in tr_d[1]]
training_data = zip(training_inputs, training_results)
validation_inputs = [np.reshape(x, (784, 1)) for x in va_d[0]]
validation_data = zip(validation_inputs, va_d[1])
test_inputs = [np.reshape(x, (784, 1)) for x in te_d[0]]
test_data = zip(test_inputs, te_d[1])
return (training_data, validation_data, test_data)
def vectorized_result(j):
"""Вернуть 10-мерный единичный вектор с 1.0 в позиции j и нулями на остальных позициях. Это используется для преобразования цифры (0..9) в соответствующие выходные данные НС."""
e = np.zeros((10, 1))
e[j] = 1.0
return e
Я говорил, что наша программа достигает довольно неплохих результатов. Что это означает? Неплохих по сравнению с чем? Полезно бывает иметь результаты неких простых, базовых испытаний, с которыми можно было бы провести сравнение, чтобы понять, что значит «хорошие результаты». Простейшим базовым уровнем, конечно, будет случайная догадка. Это можно делать примерно в 10% случаев. А мы показываем гораздо лучший результат!
Что насчёт менее тривиального базового уровня? Давайте посмотрим на то, насколько темна картинка. К примеру, изображение 2 обычно будет темнее изображения 1, просто потому, что у неё больше тёмных пикселей, как видно на примерах ниже:

Из этого следует, что мы можем вычислить среднюю темноту для каждой цифры от 0 до 9. Получая новое изображение, мы вычисляем его темноту, и догадываемся, что на нём изображена цифра с ближайшей средней темнотой. Это простая процедура, которую легко запрограммировать, поэтому код я писать не буду – если интересно, он
лежит на GitHub. Но это уже серьёзное улучшение по сравнению со случайными догадками – код правильно распознаёт 2 225 из 10 000 изображений, то есть, даёт точность 22,25%.
Нетрудно разыскать и другие идеи, достигающие точности в диапазоне от 20 до 50%. Поработав ещё немного, можно превысить 50%. Но чтобы достичь гораздо большей точности, лучше использовать авторитетные алгоритмы МО. Давайте попробуем один из наиболее известных алгоритмов, метод опорных векторов или SVM. Если вам незнакомы SVM, не волнуйтесь, нам не потребуется разбираться в этих деталях. Мы просто используем библиотеку python под названием scikit-learn, обеспечивающую простой интерфейс к быстрой библиотеке на C для SVM, известную, как
LIBSVM.
Если мы запустим SVM классификатор scikit-learn на настройках по умолчанию, то получим правильную классификацию 9 435 из 10 000 (код
доступен по ссылке). Это уже большое улучшение по сравнению с наивным подходом классификации изображений по темноте. Это значит, что SVM работает примерно так же хорошо, как наша НС, только чуток похуже. В следующих главах мы познакомимся с новыми техниками, которые позволят нам улучшить наши НС настолько, что они сильно обгонят SVM.
Но и это ещё не всё. Результат 9 435 из 10 000 от scikit-learn указан для настроек по умолчанию. У SVM есть много параметров, допускающих подстройку, и можно искать параметры, улучшающие этот результат. Не буду углубляться в детали, их можно прочесть в
статье Андреаса Мюллера. Он показал, что проделав работу по оптимизации параметров, можно добиться точности не менее 98,5%. Иначе говоря, хорошо настроенная SVM ошибается лишь в одной цифре из 70. Неплохой результат! Могут ли НС достичь большего?
Оказывается, могут. На сегодня хорошо настроенная НС обгоняет любую другую известную технологию в решении MNIST, включая SVM.
Рекорд на 2013 год правильно классифицировал 9 979 из 10 000 изображений. И большую часть использованных для этого технологий мы увидим в этой книге. Такой уровень точности близок к человеческому, а, возможно, и превышает его, поскольку несколько изображений из MNIST трудно расшифровать даже человеку, к примеру:
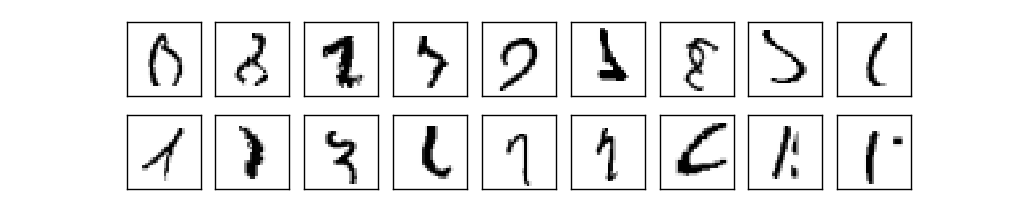
Думаю, вы согласитесь, что их сложно классифицировать! С такими изображениями в наборе данных MNIST удивительно, что НС может правильно распознать все изображения из 10 000, кроме 21. Обычно программисты считают, что для решения подобной сложной задачи требуется сложный алгоритм. Но даже НС в
работе-рекордсмене используют довольно простые алгоритмы, являющиеся небольшими вариациями тех, что мы рассмотрели в этой главе. Вся сложность автоматически появляется во время обучения на основе обучающих данных. В каком-то смысле, мораль наших результатов и тех, что содержатся в более сложных работах, в том, что для некоторых задач
сложный алгоритм ≤ простой алгоритм обучения + хорошие обучающие данные
К глубокому обучению
Хотя наша сеть демонстрирует впечатляющую эффективность, достигается она загадочным способом. Веса и смешения сети автоматически обнаруживаются. Значит, у нас нет готового объяснения того, как сеть делает то, что делает. Можно ли найти какой-то способ понять базовые принципы классификации сетью рукописных цифр? И можно ли, учитывая их, улучшить результат?
Переформулируем эти вопросы более жёстко: допустим, что через несколько десятилетий НС превратятся в искусственный интеллект (ИИ). Поймём ли мы, как этот ИИ работает? Возможно, сети останутся непонятными для нас, с их весами и смещениями, поскольку они назначаются автоматически. В ранние годы исследований ИИ люди надеялись, что попытки создания ИИ также помогут нам понять принципы, лежащие в основе интеллекта, и, может быть, даже работы человеческого мозга. Однако в итоге может оказаться, что мы не будем понимать ни мозг, ни то, как работает ИИ!
Чтобы разобраться с этими вопросами, давайте вспомним об интерпретации искусственных нейронов, данной мною в начале главы – что это способ взвешивать свидетельства. Допустим, мы хотим определить, есть ли на изображении лицо человека:



К этой проблеме можно подходить так же, как к распознаванию рукописного ввода: используя пиксели изображений в качестве входных данных для НС, а на выходе НС будет один нейрон, который будет говорить, «Да, это лицо», или «Нет, это не лицо».
Допустим, мы сделаем это, но не используя алгоритм обучения. Мы попробуем вручную создать сеть, выбирая подходящие веса и смещения. Как мы можем к этому подступиться? Забыв на минуту о НС, мы могли бы разбить задачу на подзадачи: есть ли у изображения глаз в левом верхнем углу? Есть ли глаз в правом верхнем углу? Есть ли посередине нос? Есть ли внизу посередине рот? Есть ли вверху волосы? И так далее.
Если ответы на несколько из этих вопросов положительные, или даже «вероятно, да», тогда мы заключаем, что на изображении, возможно, есть лицо. И наоборот, если ответы отрицательные, то лица, вероятно, нет.
Это, конечно, примерная эвристика, и у неё множество недостатков. Возможно, это лысый человек, и у него нет волос. Возможно, нам видна только часть лица, или лицо под углом, так что некоторые части лица закрыты. И всё же эвристика говорит о том, что если мы можем решить подзадачи при помощи нейросетей, то, возможно, мы можем создать НС для распознавания лиц, комбинируя сети для подзадач. Ниже приведена возможная архитектура такой сети, в которой прямоугольниками обозначены подсети. Это не совсем реалистичный подход к решению задачи распознавания лиц: он нужен, чтобы помочь нам интуитивно разобраться в работе нейросетей.
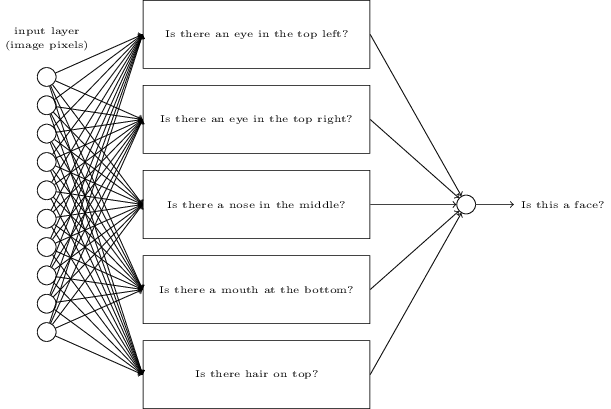 В прямоугольниках – подзадачи: есть ли у изображения глаз в левом верхнем углу? Есть ли глаз в правом верхнем углу? Есть ли посередине нос? Есть ли внизу посередине рот? Есть ли вверху волосы? И так далее.
В прямоугольниках – подзадачи: есть ли у изображения глаз в левом верхнем углу? Есть ли глаз в правом верхнем углу? Есть ли посередине нос? Есть ли внизу посередине рот? Есть ли вверху волосы? И так далее.
Возможно, что и подсети тоже можно разобрать на составляющие. Возьмём вопрос с наличием глаза в левом верхнем углу. Его можно разобрать на вопросы типа: «Есть ли бровь?», «Есть ли ресницы?», «Есть ли зрачок?» и так далее. Конечно, в вопросах должна содержаться информация о расположении – «Расположена ли бровь слева вверху, над зрачком?», и так далее – но давайте пока упростим. Поэтому сеть, отвечающую на вопрос о наличии глаза, можно разобрать на составляющие:
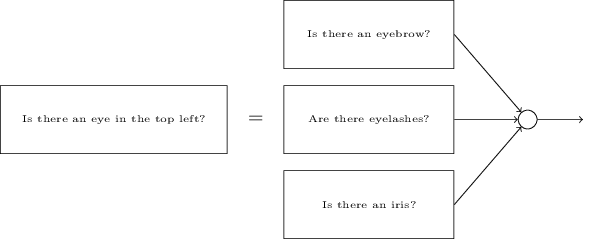 «Есть ли бровь?», «Есть ли ресницы?», «Есть ли зрачок?»
«Есть ли бровь?», «Есть ли ресницы?», «Есть ли зрачок?»
Эти вопросы можно дальше разбивать на мелкие, по шагам через многие слои. В итоге мы будем работать с подсетями, отвечающие на такие простые вопросы, что их легко можно разобрать на уровне пикселей. Эти вопросы могут касаться, к примеру, наличия или отсутствия простейших форм в определённых местах изображения. На них смогут ответить отдельные нейроны, связанные с пикселями.
В итоге получится сеть, разбивающая очень сложные вопросы – наличие на изображении лица – на очень простые вопросы, на которые можно отвечать на уровне отдельных пикселей. Она будет делать это через последовательность из многих слоёв, в которых первые слои отвечают на очень простые и конкретные вопросы об изображении, а последние создают иерархию из более сложных и абстрактных концепций. Сети с такой многослойной структурой – двумя или большим количеством скрытых слоёв – называются глубокими нейросетями (ГНС).
Конечно, я не говорил о том, как сделать это рекурсивное разбиение по подсетям. Определённо непрактично будет вручную подбирать веса и смещения. Мы бы хотели использовать обучающие алгоритмы, чтобы сеть автоматически обучалась весам и смещениям – а через них и иерархии концепций – на основе обучающих данных. Исследователи в 1980-х и 1990-х пытались использовать стохастический градиентный спуск и обратное распространение для тренировки ГНС. К сожалению, за исключением нескольких особых архитектур, у них ничего не получилось. Сети обучались, но очень медленно, и на практике это было слишком медленно для того, чтобы это можно было как-то использовать.
С 2006 года было разработано несколько технологий, позволяющих обучать ГНС. Они основаны на стохастическом градиентном спуске и обратном распространении, но содержат и новые идеи. Они позволили обучать гораздо более глубокие сети – сегодня люди спокойно обучают сети с 5-10 слоями. И оказывается, что они гораздо лучше решают многие проблемы, чем неглубокие НС, то есть сети с одним скрытым слоем. Причина, конечно, в том, что ГНС могут создавать сложную иерархию концепций. Это похоже на то, как языки программирования используют модульные схемы и идеи абстракций, чтобы на них можно было создавать сложные компьютерные программы. Сравнивать глубокую НС с неглубокой НС – примерно как сравнивать язык программирования, умеющий делать вызовы функций, с языком, этого не умеющим. Абстракция в НС выглядит не так, как в языках программирования, но имеет такую же важность.
 Перед вами – перевод свободной онлайн-книги Майкла Нильсена «Neural Networks and Deep Learning», распространяемой под лицензией Creative Commons Attribution-NonCommercial 3.0 Unported License. Мотивацией к его созданию послужил успешный опыт перевода учебника по программированию, "Выразительный JavaScript". Книга по нейросетям тоже достаточно популярна, на неё активно ссылаются авторы англоязычных статей. Её переводов я не нашёл, за исключением перевода начала первой главы с сокращениями.
Перед вами – перевод свободной онлайн-книги Майкла Нильсена «Neural Networks and Deep Learning», распространяемой под лицензией Creative Commons Attribution-NonCommercial 3.0 Unported License. Мотивацией к его созданию послужил успешный опыт перевода учебника по программированию, "Выразительный JavaScript". Книга по нейросетям тоже достаточно популярна, на неё активно ссылаются авторы англоязычных статей. Её переводов я не нашёл, за исключением перевода начала первой главы с сокращениями.