• Тестирование веб-сервисов
• Машинное обучение
• Математика
• Python
• Блог компании Open Data Science

Здравствуйте, коллеги. Рассмотрим обычный онлайн-эксперимент в некоторой компании «Усы и когти». У неё есть веб-сайт, на котором есть красная кнопка в форме прямоугольника с закругленными краями. Если пользователь нажимает на эту кнопку, то где-то в мире мурлычет от радости один котенок. Задача компании — максимизация мурлыкания. Также есть отдел маркетинга, который усердно исследует формы кнопок и то, как они влияют на конверсию показов в клико-мурлыкания. Потратив почти весь бюджет компании на уникальные исследования, отдел маркетинга разделился на четыре противоборствующие группировоки. У каждой группировки есть своя гениальная идея того, как должна выглядеть кнопка. В целом никто не против формы кнопки, но красный цвет раздражает всех маркетологов, и в итоге было предложено четыре альтернативных варианта. На самом деле, даже не так важно, какие именно это варианты, нас интересует тот вариант, который максимизирует мурлыкания. Маркетинг предлагает провести A/B/n-тест, но мы не согласны: и так на эти сомнительные исследования спущено денег немерено. Попробуем осчастливить как можно больше котят и сэкономить на трафике. Для оптимизации трафика, пущенного на тесты, мы будем использовать шайку многоруких байесовских бандитов (bayesian multi-armed bandits). Вперед.

A/B/n-тест

Будем считать, что клик — это некоторая случайная переменная $$, принимающая значения $$ или $$ с вероятностями $$ и $$ соответственно. Такая величина имеет распределение Бернулли с параметром $$:

Вспомним, что среднее значение распределения Бернулли равно $$, а дисперсия равна $$.

Попробуем для начала решить проблему с помощью обычного A/B/n-теста, n здесь означает, что тестируются не две гипотезы, а несколько. В нашем случае это пять гипотез. Но мы рассмотрим сначала ситуацию тестирования старого решения против нового, а затем обобщим на все пять случаев. В бинарном случае у нас есть две гипотезы:

• нулевая гипотеза $$ заключается в том, что нет никакой разницы в вероятности клика по старой кнопке $$ или по новой $$;
• альтернативная гипотеза $$ заключается в том, что вероятность клика по старой кнопке $$ меньше чем по новой $$;
• вероятности $$ и $$ мы оцениваем как отношение кликов к показам в контрольной группе (control) и в экспериментальной/тестовой группе (treatment) соответственно.

Мы не можем знать истинное значение конверсии $$ на текущей вариации кнопки (на красной), но мы можем его оценить. Для этого у нас есть два механизма, которые работают сообща. Во-первых, это закон больших чисел, который утверждает, что какое бы ни было распределение случайной величины, если мы посемплируем достаточное количество примеров и усредним, то такая оценка будет близка к истинному значению среднего значения распределения (опустим пока индекс $$ для ясности):

Во-вторых, это центральная предельная теорема, которая утверждает следующее: допустим, есть бесконечный ряд независимых и одинаково распределенных случайных величин $$, с истинным матожиданием $$ и дисперсией $$. Обозначим конечную сумму как $$, тогда

или эквивалентно тому, что при достаточно больших выборках оценка среднего значения имеет нормальное распределение с центром в $$ и дисперсией $$:

Казалось бы, бери да запускай два теста: раздели трафик на две части, жди пару дней, и сравнивай средние значения кликов по первому механизму. Второй механизм позволяет нам применять t-тест для оценки статистической значимости разницы средних значений выборок (потому что оценки средних имеют нормальное распределение). А также, увеличивая размер выборки $$, мы уменьшаем дисперсию оценки среднего, тем самым увеличивая свою уверенность. Но остается один важный вопрос: а какое количество трафика (пользователей) пустить на каждую вариацию кнопки? Статистика нам говорит, что если разница не нулевая, то это еще совсем не значит, что значения не равны. Возможно, просто не повезло, и первые $$ пользователей люто ненавидели какой-то цвет, и нужно подождать еще. И возникает вопрос, а сколько пользователей пустить на каждую вариацию кнопки, чтобы быть уверенным, что если разница и есть, то она существенная. Для этого нам придется еще раз встретиться с отделом маркетинга и задать им несколько вопросов, и, вероятно, нам придется им объяснить, что такое ошибки первого и второго рода. В общем, это может быть чуть ли не самым сложным во всем тесте. Итак, вспомним, что это за ошибки, и определим вопросы, которые следует задать отделу маркетинга, чтобы оценить количество трафика на вариацию. В конечном счете именно маркетинг принимает окончательно решение о том, какой цвет кнопки оставить.

		Верная гипотеза
		$$	$$
Ответ теста	$$	$$ принята	$$ неверно принята (ошибка II рода)
	$$	$$ неверно отвергнута (ошибка I рода)	$$ отвергнута

Введем еще несколько понятий. Обозначим вероятность ошибки первого рода как $$, т.е. вероятность принятия альтернативной гипотезы при условии, что на самом деле верна нулевая гипотеза. Эта величина называется статистической значимостью (statistical significance). Также нам понадобится ввести вероятность ошибки второго рода $$. Величина $$ называется статистической мощностью (statistical power).

Рассмотрим изображение ниже, чтобы проиллюстрировать смысл статистической значимости и мощности. Предположим, что среднее значение распределения случайной величины на контрольной группе равно $$, а на тестовой $$. Выберем некоторый критический порог выше которого гипотеза $$ отвергается (вертикальная зеленая линия). Тогда если значение было правее порога, но из распределения контрольной группы, то мы его ошибочно припишем к распределению тестовой группы. Это будет ошибка первого рода, а значение $$ — это площадь, закрашенная красным цветом. Соответственно, площадь области, закрашенной синим цветом, равна $$. Величина $$, которую мы назвали статистической мощностью, по сути показывает, сколько значений, соответствующих альтернативной гипотезе, мы действительно отнесем к альтернативной гипотезе. Проиллюстрируем вышеописанное.

# средние значение двух распределений
mu_c = 0.1
mu_t = 0.6

# дисперсии двух распределений
s_c = 0.25
s_t = 0.3

# порог: наблюдая значение исследуемой величины выше этого порога,
# мы относим ее к синему распределению
c = 1.3*(mu_c + mu_t)/2

support = np.linspace(
    stats.norm.ppf(0.0001, loc=mu_c, scale=s_c), 
    stats.norm.ppf(1 - 0.0005, loc=mu_t, scale=s_t), 1000)
y1 = stats.norm.pdf(support, loc=mu_c, scale=s_c)
y2 = stats.norm.pdf(support, loc=mu_t, scale=s_t)

fig, ax = plt.subplots()
ax.plot(support, y1, color='r', label='y1: control')
ax.plot(support, y2, color='b', label='y2: treatment')
ax.set_ylim(0, 1.1*np.max([
            stats.norm.pdf(mu_c, loc=mu_c, scale=s_c),
            stats.norm.pdf(mu_t, loc=mu_t, scale=s_t)
        ]))
ax.axvline(c, color='g', label='c: critical value')
ax.axvline(mu_c, color='r', alpha=0.3, linestyle='--', label='mu_c')
ax.axvline(mu_t, color='b', alpha=0.3, linestyle='--', label='mu_t')
ax.fill_between(support[support <= c], 
                y2[support <= c], 
                color='b', alpha=0.2, label='b: power')
ax.fill_between(support[support >= c], 
                y1[support >= c], 
                color='r', alpha=0.2, label='a: significance')

ax.legend(loc='upper right', prop={'size': 20})
ax.set_title('A/B test setup for sample size estimation', fontsize=20)
ax.set_xlabel('Values')
ax.set_ylabel('Propabilities')

plt.show()

Обозначим этот порог буквой $$. Справедливо следующее равенство при условии, что случайная величина имеет нормальное распределение:

где $$ — это квантильная функция.

В нашем случае мы можем записать систему из двух уравнений для $$ и $$ соответственно:

Решив эту систему относительно $$, мы получим оценку достаточного количества трафика, который необходимо загнать в каждый эксперимент при заданной статистической значимости и мощности.

Например, если реальное значение конверсии $$, а новое $$, тогда при $$ нам необходимо прогнать 2 269 319 пользователей через каждую вариацию. А новая вариация будет принята в случае, если ее конверсия превысит $$. Проверим это.

def get_size(theta_c, theta_t, alpha, beta):
    # вычисляем квантили нормального распределения
    t_alpha = stats.norm.ppf(1 - alpha, loc=0, scale=1)
    t_beta = stats.norm.ppf(beta, loc=0, scale=1)
    # решаем уравнение относительно n
    n = t_alpha*np.sqrt(theta_t*(1 - theta_t))
    n -= t_beta*np.sqrt(theta_c*(1 - theta_c))
    n /= theta_c - theta_t
    return int(np.ceil(n*n))

n_max = get_size(0.001, 0.0011, 0.01, 0.01)
print n_max
# выводим порог, выше которого отклоняется H_0
print 0.001 + stats.norm.ppf(1 - 0.01, loc=0, scale=1)*np.sqrt(0.001*(1 - 0.001)/n_max)

>>>2269319
>>>0.00104881009215

Таким образом, чтобы вычислить эффективный размер выборки, мы должны пойти в маркетинг или другой бизнес-департамент и узнать у них следующее:

• какое значение конверсии $$ на новой вариации должно получиться, чтобы бизнес принял решение перейти со старой версии кнопки с конверсией $$ на новую; естественно предположить, что если новое больше старого, то уже достаточно оснований для внедрения, но не стоит забывать про накладные расходы, как минимум на тестирование, ведь чем меньше разница, тем больше трафика нужно потратить на тест, а это потеря прибыли (при этом существует риск, что тест провалится);
• какой допустимый уровень значимости $$ и мощности $$ необходим (вероятно, тут еще придется как то объяснить бизнесу, что это значит).

Получив $$, мы можем легко вычислить порог $$. Это значит, что если мы соберем $$ наблюдений для каждой вариации, и окажется, что в экспериментальной группе оценка клика $$ выше порога $$, то мы отклоняем $$ и принимаем альтернативную гипотезу $$ о том, что новая вариация лучше и вероятно мы ее внедрим. В этом случае у нас будет $$ шансов ошибки первого рода, т.е. мы ошибочно приняли решение заменить старую кнопку на новую. И $$ шансов, что если новая вариация лучше, то мы правильно и сделали, что ее внедрили. Но самое печальное в том, что если после эксперимента, когда мы прогнали трафик через две вариации, окажется, что $$, то мы считаем, что нет оснований отказываться от старой кнопки. Именно нет основания, мы не доказали, что новая кнопка хуже: мы как были в неопределенности, так и остались. Такие дела.

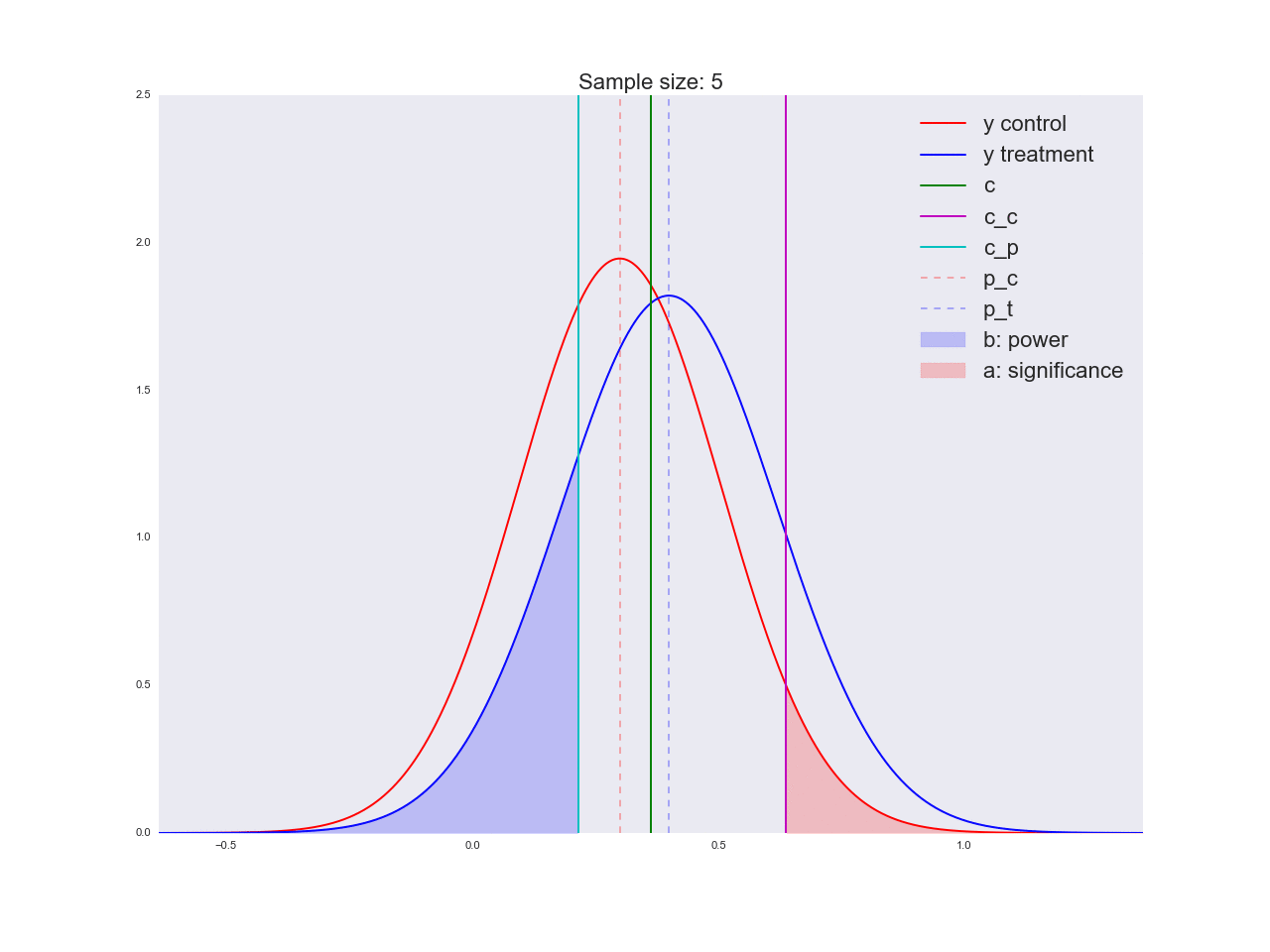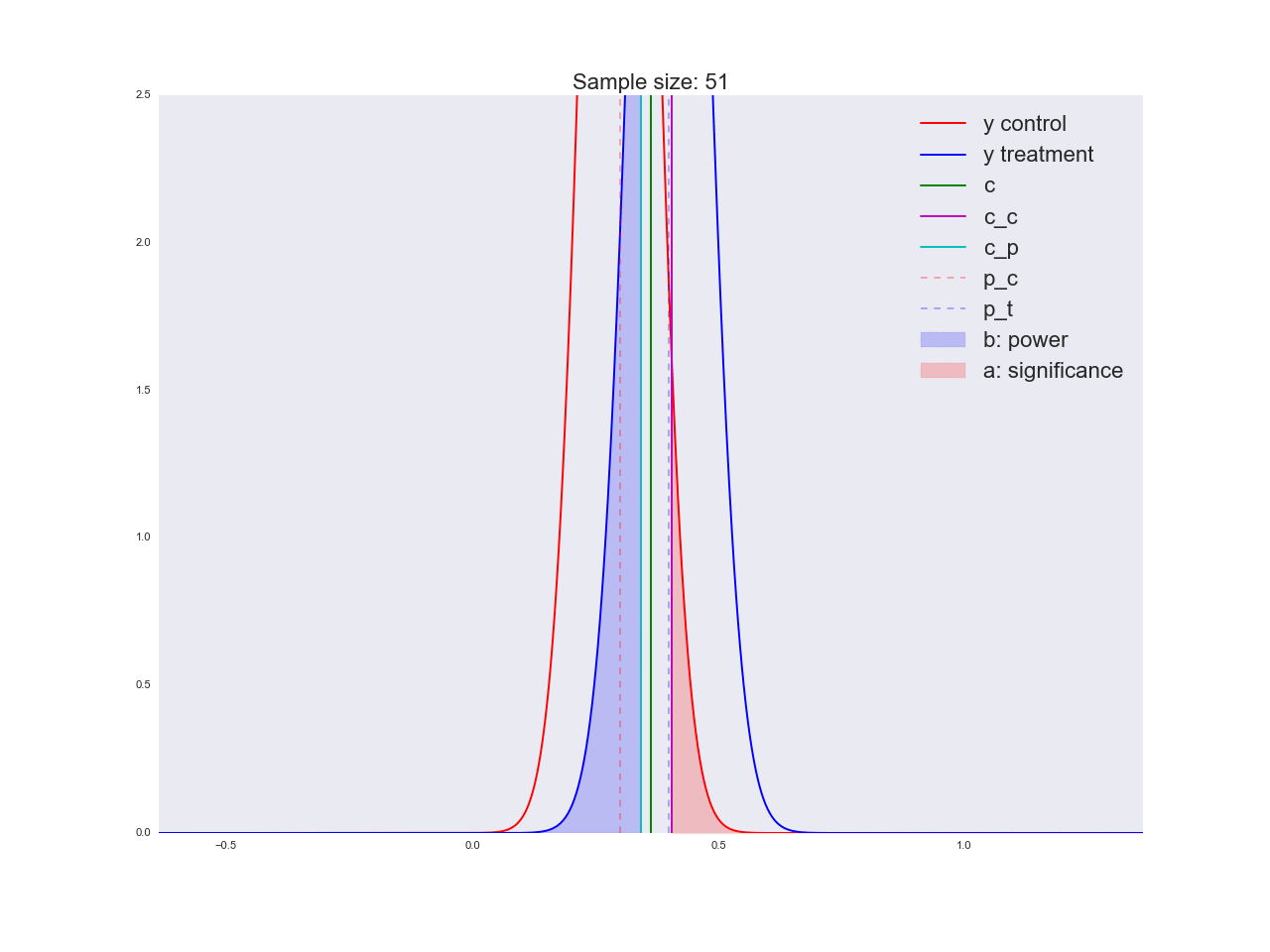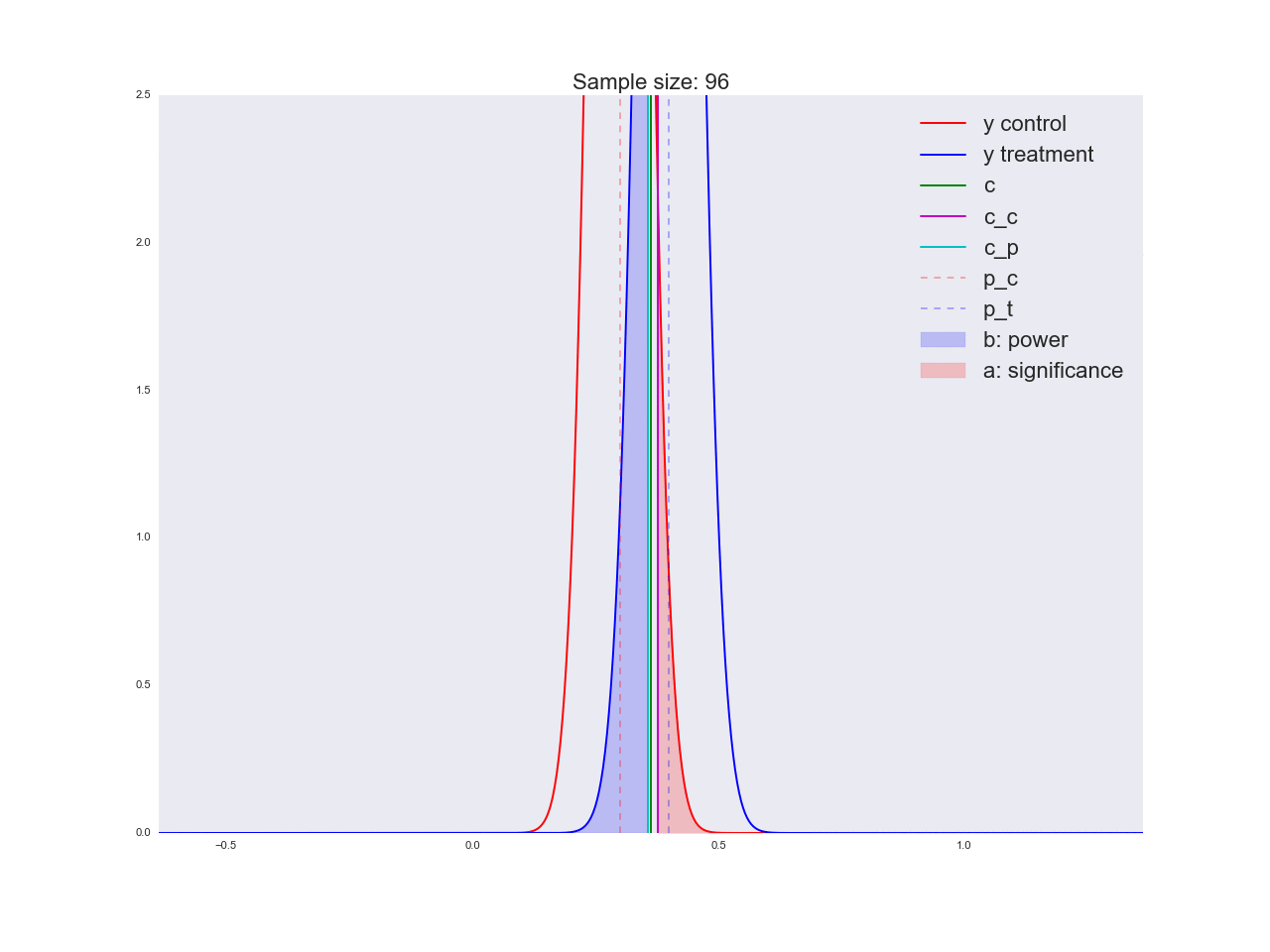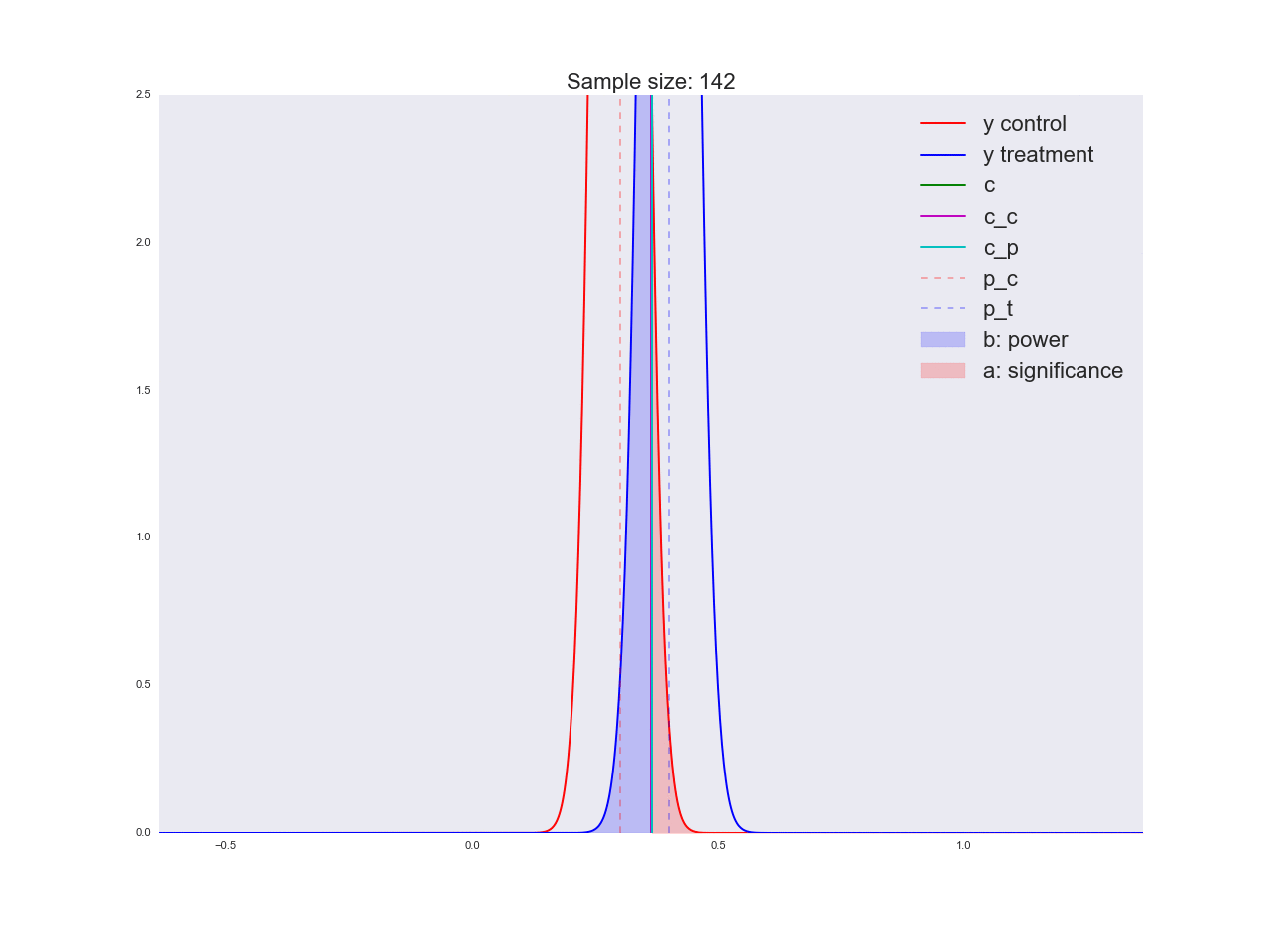
Честно говоря, мне кажется, что выводы, полученные в предыдущем абзаце, не очень убедительны, и вообще могут запутать не только вас. Представьте, что отдел маркетинга потратил пару миллионов рублей на уникальные исследования новой формы кнопки, а вы им такой «нет оснований считать, что она лучше». Кстати насчет, оснований: давайте проиллюстрируем, как решается уравнение относительно размера выборки и как изменяется распределение оценки среднего значения при увеличении размера выборки. На анимации вы можете наблюдать, как при увеличении размера выборки размах распределения оценки среднего уменьшается, т.е. уменьшается дисперсия оценки, которая и отождествляется с нашей уверенностью в этой оценке. На самом деле, изображение ниже немного нечестное: при уменьшении размаха распределения, оно еще и увеличивается в высоту, т.к. площадь должна оставаться постоянной.

np.random.seed(1342)

p_c = 0.3 
p_t = 0.4
alpha = 0.05
beta = 0.2

n_max = get_size(p_c, p_t, alpha, beta)
c = p_c + stats.norm.ppf(1 - alpha, loc=0, scale=1)*np.sqrt(p_c*(1 - p_c)/n_max)
print n_max, c

def plot_sample_size_frames(do_dorm, width, height):
    left_x = c - width
    right_x = c + width

    n_list = range(5, n_max, 1) + [n_max]
    for f in glob.glob("./../images/sample_size_gif/*_%s.*" % 
                       ('normed' if do_dorm else 'real')):
        os.remove(f)
    for n in tqdm_notebook(n_list):
        s_c = np.sqrt(p_c*(1 - p_c)/n)
        s_t = np.sqrt(p_t*(1 - p_t)/n)

        c_c = p_c + stats.norm.ppf(1 - alpha, loc=0, scale=1)*s_c
        c_t = p_t + stats.norm.ppf(beta, loc=0, scale=1)*s_t

        support = np.linspace(left_x, right_x, 1000)
        y_c = stats.norm.pdf(support, loc=p_c, scale=s_c)
        y_t = stats.norm.pdf(support, loc=p_t, scale=s_t)
        if do_dorm:
            y_c /= max(y_c.max(), y_t.max())
            y_t /= max(y_c.max(), y_t.max())

        fig, ax = plt.subplots()
        ax.plot(support, y_c, color='r', label='y control')
        ax.plot(support, y_t, color='b', label='y treatment')

        ax.set_ylim(0, height)
        ax.set_xlim(left_x, right_x)

        ax.axvline(c, color='g', label='c')
        ax.axvline(c_c, color='m', label='c_c')
        ax.axvline(c_t, color='c', label='c_p')
        ax.axvline(p_c, color='r', alpha=0.3, linestyle='--', label='p_c')
        ax.axvline(p_t, color='b', alpha=0.3, linestyle='--', label='p_t')

        ax.fill_between(support[support <= c_t], 
                        y_t[support <= c_t], 
                        color='b', alpha=0.2, label='b: power')
        ax.fill_between(support[support >= c_c], 
                        y_c[support >= c_c], 
                        color='r', alpha=0.2, label='a: significance')

        ax.legend(loc='upper right', prop={'size': 20})

        ax.set_title('Sample size: %i' % n, fontsize=20)

        fig.savefig('./../images/sample_size_gif/%i_%s.png' % 
                    (n, 'normed' if do_dorm else 'real'), dpi=80)

        plt.close(fig)

plot_sample_size_frames(do_dorm=True, width=0.5, height=1.1)
plot_sample_size_frames(do_dorm = False, width=1, height=2.5)

!convert -delay 5 $(for i in $(seq 5 1 142); do echo ./../images/sample_size_gif/${i}_normed.png; done) -loop 0 ./../images/sample_size_gif/sample_size_normed.gif
for f in glob.glob("./../images/sample_size_gif/*_normed.png"):
    os.remove(f)

!convert -delay 5 $(for i in $(seq 5 1 142); do echo ./../images/sample_size_gif/${i}_real.png; done) -loop 0 ./../images/sample_size_gif/sample_size_real.gif
for f in glob.glob("./../images/sample_size_gif/*_real.png"):
    os.remove(f)

Читерская анимация:

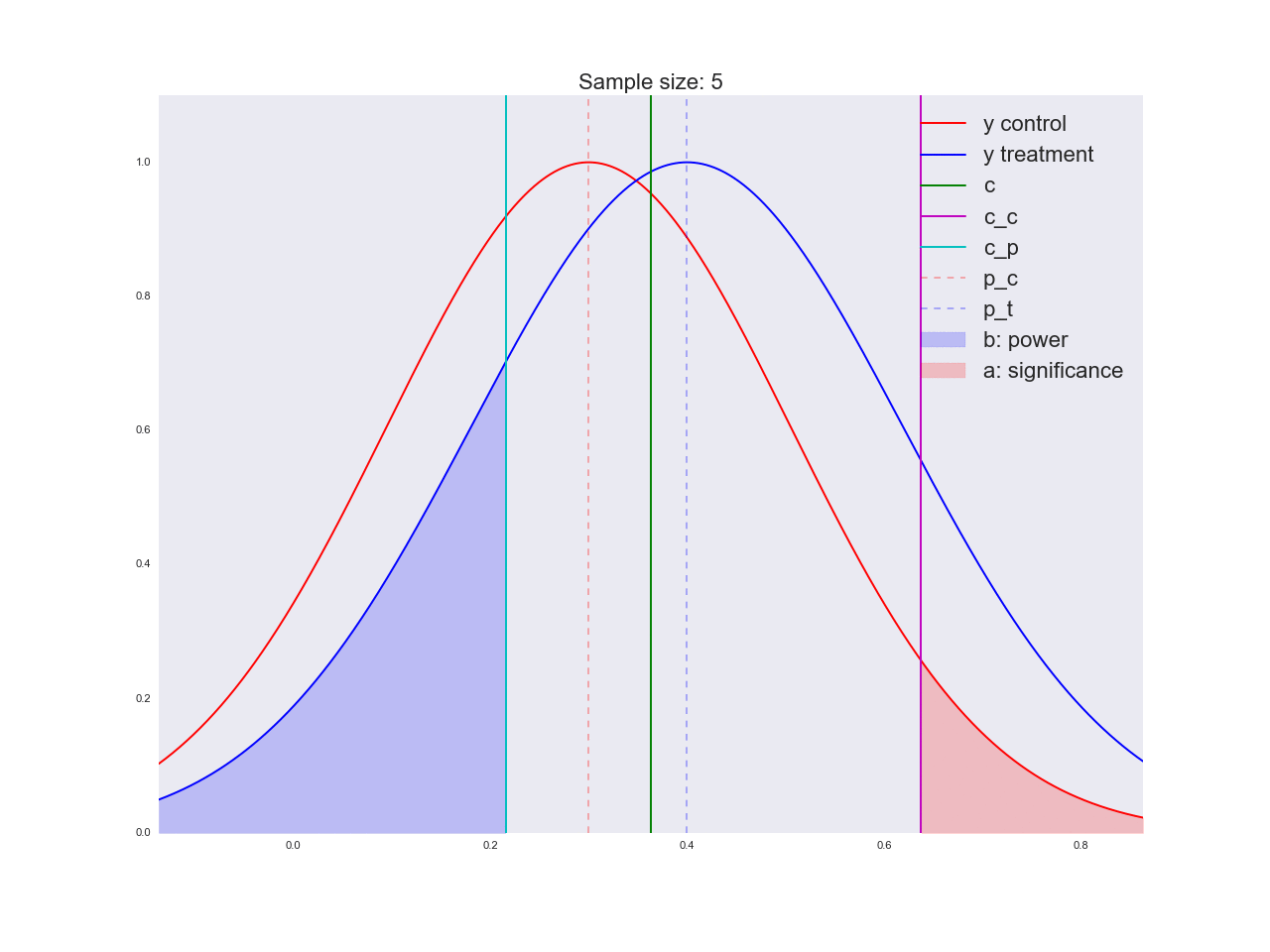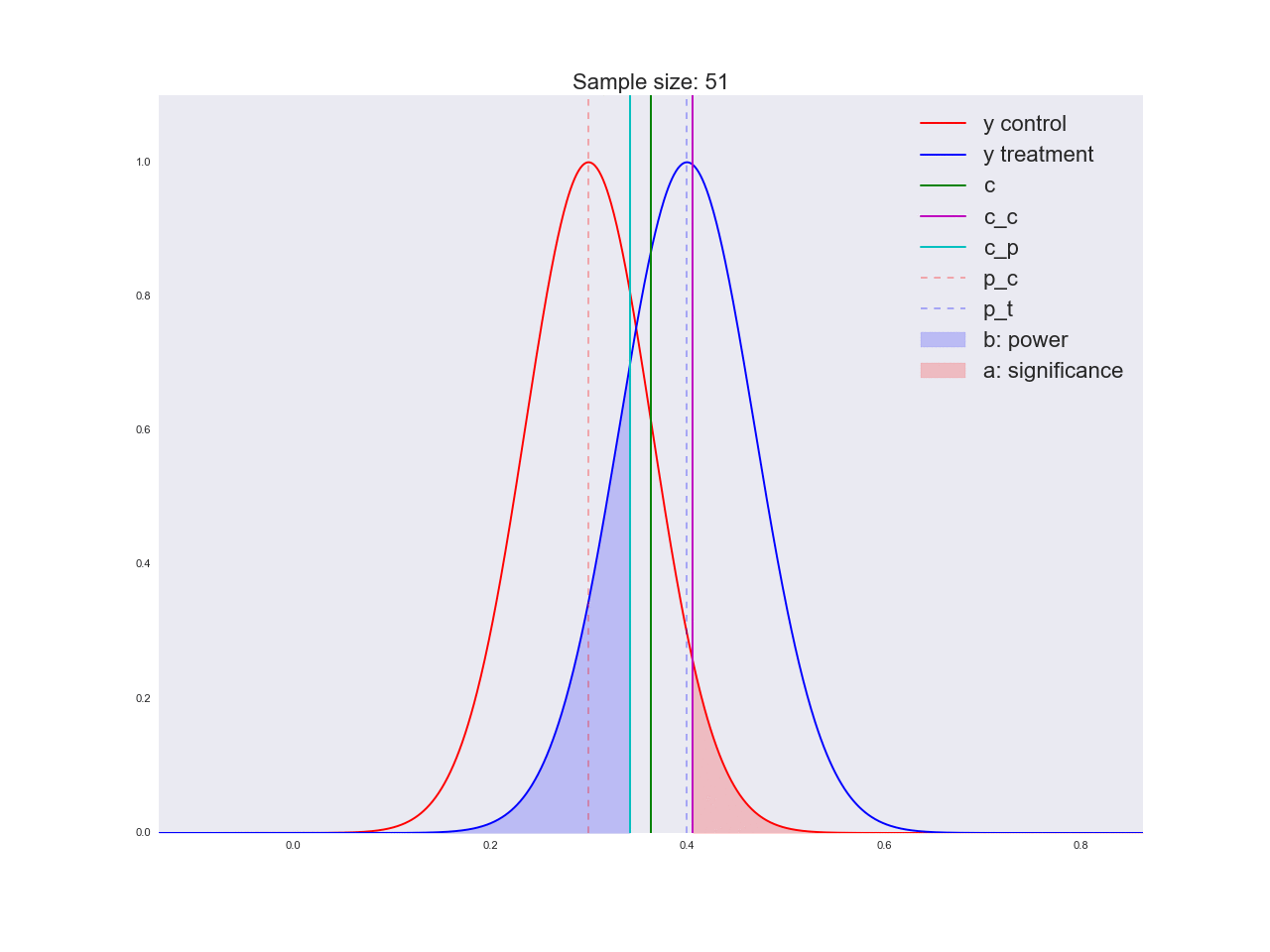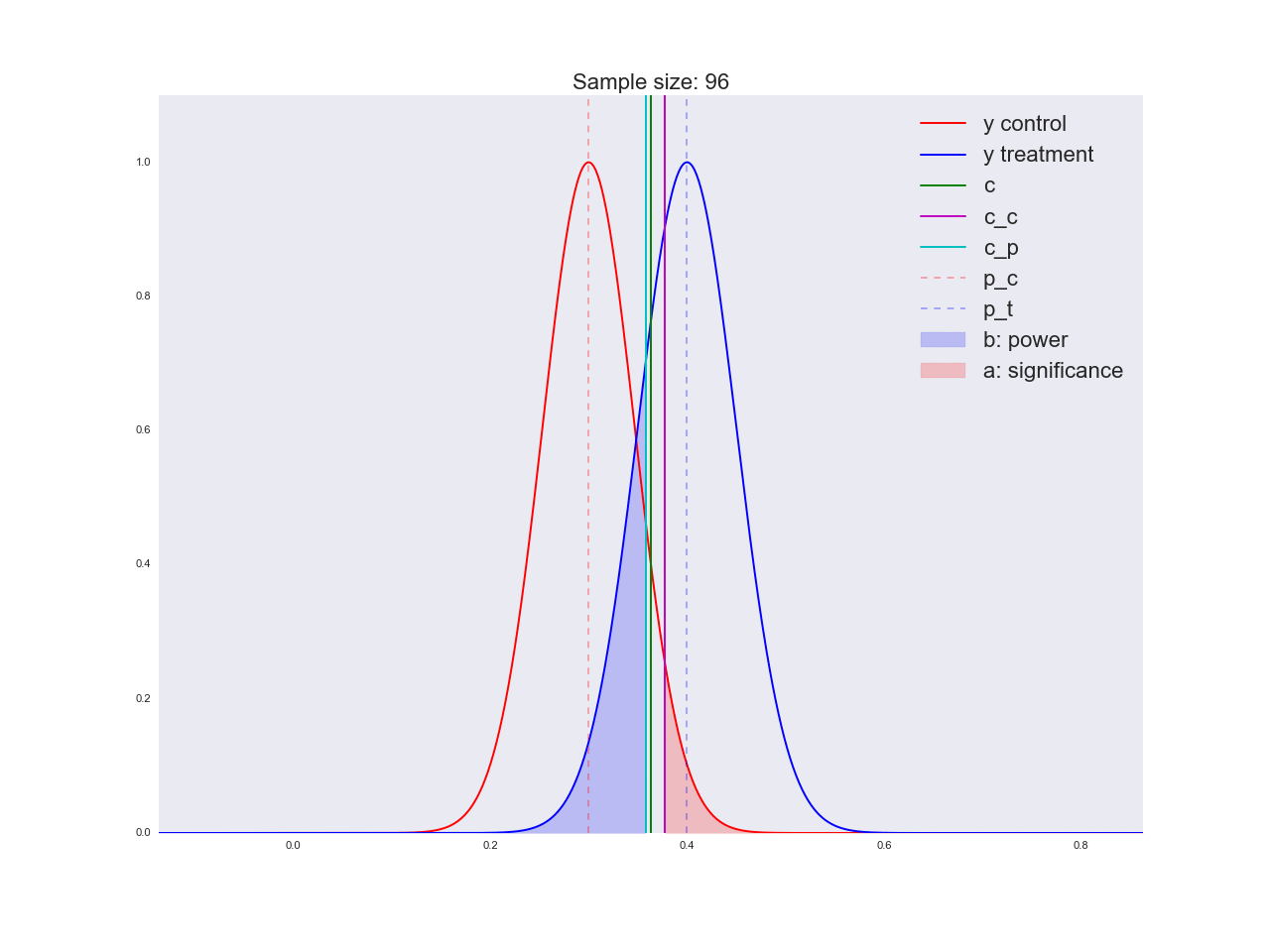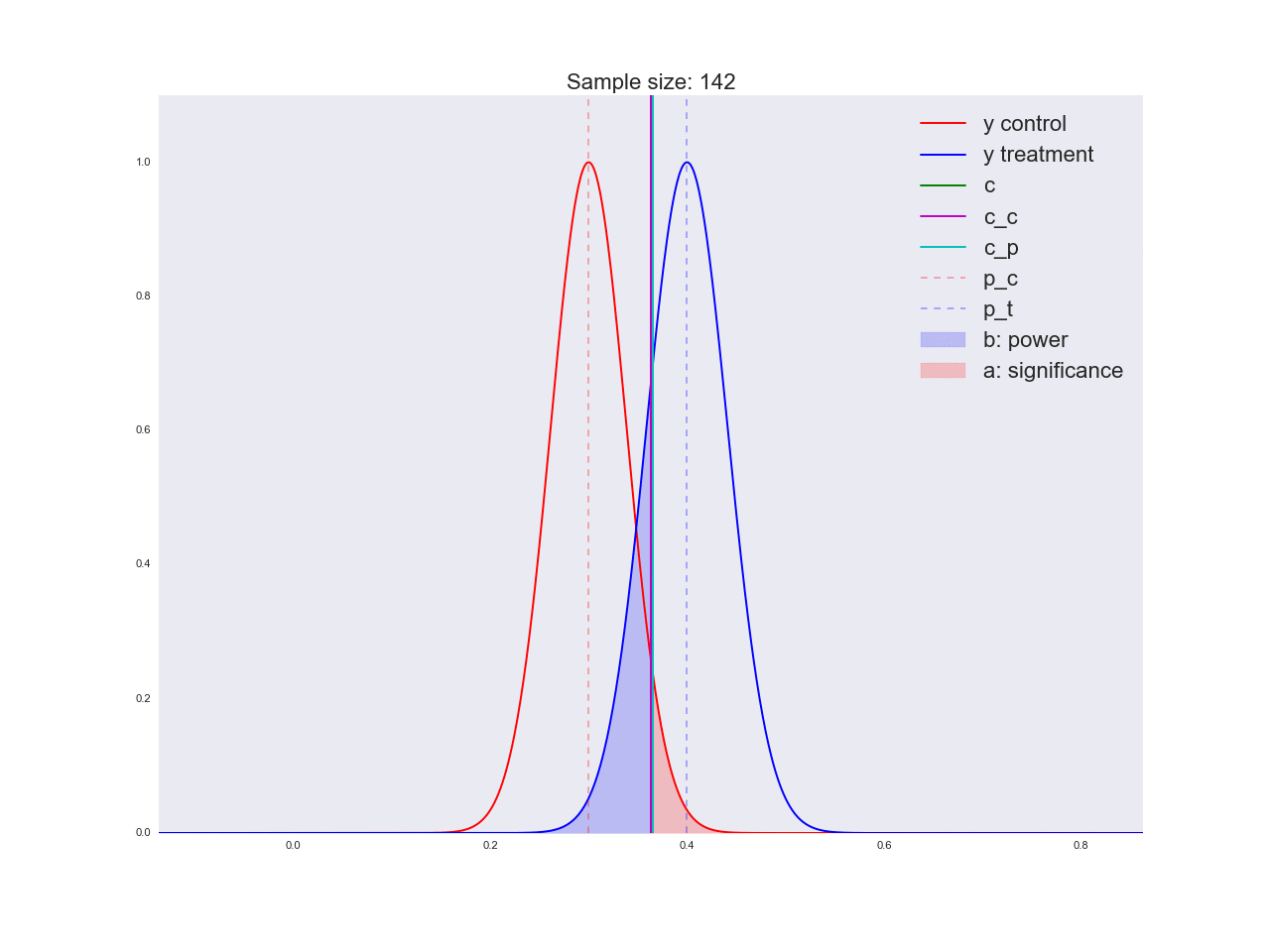
Реальная анимация:

В завершении раздела про A/B/n-тесты поговорим про n. Мы же в самом начале говорили, что у нас помимо текущей вариации есть четыре альтернативные гипотезы. Вышеописанный дизайн эксперимента легко масштабируется на n вариаций, в нашем случае их всего 5. Не поменяется ровным счетом ничего, кроме того, что теперь мы трафик разделяем на 5 частей и исследуем отклонение хотя бы одной из них выше критического порога $$. Но мы то с вами точно знаем, что лучшим вариантом является только один вариант, а это значит, что мы направляем $$ (где $$ — количество вариаций) на заведомо плохие вариации, мы просто пока не знаем, какие из них — плохие. А каждый пользователь, направленный на плохую вариацию, приносит нам меньше прибыли, чем если бы он был направлен на хорошую вариацию. В следующем разделе мы рассмотрим альтернативную методику дизайна экспериментов, которая крайне эффективна именно в онлайн-тестировании.

Ну и чтобы окончательно вас добить сложностями проведения A/B/n-тестов, рассмотрим одну из возможных поправок значимости результата при множественном тестировании гипотез. Например, мы решили, что $$, а тестов в эксперименте пять, тогда:

Получается, что если даже все тесты не значимы, то все равно $$ шансов, что мы ошибочно получим значимый результат. Неожиданно, правда? Попробуем разобраться. Допустим, у нас есть $$ тестов в рамках одного эксперимента. Для каждого заданы свои p-values $$ (вероятность ошибочно отклонить $$, а это и есть наши $$). Что если мы уменьшим уровни значимости в $$ раз:

Тогда вероятность того, что хотя бы один результат значим, будет наше исходное $$. Проверим:

Такой трюк называется поправкой Холма-Бонферонни. Таким образом, чем больше гипотез, тем меньше требуемый уровень значимости, тем больше пользователей нужно нагнать в каждый тест. Возвращаясь к предыдущему примеру, отметим, что нам было необходимо 2 269 319 пользователей, но с поправкой нужно 2 853 873 пользователей на каждую вариацию. А это, на минуточку, почти на $$ больше трафика на весь эксперимент. Если углубиться во все возможные поправки, то получится на небольшую книжку по статистике. Такие дела.

История про зомби-лосося

В 2012 году ряд авторов получили Шнобелевскую премию по нейробиологии за то, что при помощи сложных инструментов и простой статистики могут обнаружить релевантную мозговую активность даже в мёртвом лососе. Как так? Началось все с того, что авторам нужно было протестировать аппарат МРТ. Обычно для этого берется шар, наполненный маслом и сканируется. Но авторы решили, что это как-то банально и не весело. Один из них приобрел на рынке целую тушку атлантического лосося. Рыбку положили в аппарат МРТ и стали демонстрировать ему изображения с людьми в повседневной жизни.

Задача то была в общем показать, что в мозгу дохлого лосося не происходит никакой активности при демонстрации ему изображений с людьми. Аппарат МРТ возвращает огромный массив данных, атомарной единицей там являются воксели — по сути небольшой куб данных, на которые разбивается сканируемый объект. Для того чтобы исследовать активность мозга в целом, необходимо провести множественное тестирование гипотез относительно каждого вокселя (похоже на наше тестирование, но только тестов сильно больше). И оказалось, что если не делать поправку Бонферонни, то получается, что у лосося существует корреляция между стимулами и реакцией мозга, т.е. мертвый лосось реагирует на стимулы. Но если сделать поправку, то мертвый лосось остается мертвым.

Многие думают, что Шнобелевская премия это просто приколы, но именно эта работа внесла реальный вклад в науку. Авторы проанализировали статьи по нейробиологии до 2010 года и оказалось, что около 40 процентов авторов не используют поправку в множественном тестировании гипотез. После публикации статьи про лосось, количество статей в нейробиологии, которые не используют поправку, упало до 10 процентов.

Байесовские многорукие бандиты

Сразу стоит отметить, бандиты не являются универсальной заменой A/B-тестированию, но являются отличной заменой в определенных областях. A/B-тестирование появилось больше века назад, и за все время применялось для тестирования гипотез в различных областях, таких как медицина, сельское хозяйство, экономика и т. д. У всех этих областей есть несколько общих факторов:

• стоимость одного эксперимента существенна (представьте какое-нибудь новое средство от страшной болезни: помимо того, чтобы его произвести, необходимо еще найти людей, которые согласятся принимать таблетку, не зная, является она лекарством или плацебо);
• ошибки обходятся крайне дорого (опять же, факт из медицины: если фарм-компания спустя 10 лет исследований выпустит на рынок средство, которое не работает, вероятно, этой фарм-компании конец, а также людям, которые ей доверились).

A/B-тестирование идеально подходит для классических экспериментов. Оно позволяет оценить размер выборки для теста, что позволяет также заранее оценить бюджет. А также оно позволяет задать необходимые уровни ошибки: скажем, медики могут поставить крайне небольшие $$ и $$, в то время как других не так волнует мощность, но волнует значимость. Например, при тестировании нового рецепта бургеров мы не хотим подавать новое, если оно реально хуже старого; но если мы ошиблись в другую сторону, т.е. новый рецепт лучше, но мы его не приняли, то это мы легко переживем, т.к. до сегодняшнего дня мы ведь как-то жили с этим и не разорились. Вопрос только упирается в бюджет, который мы готовы потратить на эксперимент, если он у нас бесконечен, то, конечно, нам проще приблизить оба порога к нулю и прогнать миллионы экспериментов.

Но в мире онлайн-экспериментов всё не так критично, как в классических экспериментах. Цена ошибки близка к нулю, цена эксперимента тоже близка к нулю. Да, это не исключает того, что можно применять A/B-тесты. Но есть вариант лучше, который не просто тестирует гипотезы и дает ответ, какая из них, возможно, лучше, а ещё и динамически изменяет свои оценки того, какая вариация лучше, и, наконец, принимает решение, сколько трафика послать на ту или иную вариацию в данный момент времени.

Вообще, это один из многих компромиссов, с которым приходится жить в машинном обучении: в данном случае — это исследование других вариантов против эксплуатации лучшего (exploration vs exploitaion trade-off). В процессе тестирования двух или более гипотез (вариаций кнопки) мы не хотим посылать на заведомо неверные варианты большое количество трафика (в случае A/B-теста мы посылаем равные доли на каждую вариацию). Но в то же время, мы хотим следить и за остальными вариациями, и в случае, если нам вначале не повезло, или сменилась мода на цвета кнопок, мы бы могли почувствовать это и исправить ситуацию. На помощь к нам приходят байесовские бандиты. Вот они.

Описанный дизайн очень напоминает ситуацию, когда вы приходите в казино, и перед вами стоит ряд игральных автоматов типа «однорукий бандит». У вас ограниченное количество денег и времени, и вы хотели бы по-быстрому найти лучший автомат, при этом понеся как можно меньше расходов. Такая постановка задачи называется задачей о многоруком бандите. Существует множество подходов к этой задаче, начиная от простой $$-жадной стратегии, когда вы с вероятностью $$ дергаете за ту ручку, которая принесла вам больше всего прибыли к текущему моменту, и с вероятностью $$ вы дергаете случайную руку (имеется в виду рычаг игрового автомата). Есть более сложные способы, основанные на анализе потерь при игре неоптимальной рукой. Но мы рассмотрим другой способ, основанный на семплировании Томпсона и теореме Байеса. Способ не очень новый (1933 год), но он стал востребован только в эпоху онлайн-экспериментов. Yahoo была одной из первых компаний, которые стали использовать этот метод для персонализации новостной выдачи в начале 2010-ых годов. Позже Microsoft стал использовать бандитов для оптимизации CTR-баннеров в выдаче поиска Bing. В принципе, основная масса статей про современные онлайн-исследования пишется ими. Кстати, постановка задачи очень напоминает обучение с подкреплением, за одним лишь исключением: в постановке задачи с бандитами агент не может изменять окружение, а в общем обучении с подкреплением агент может влиять на среду.

Формализуем бандитскую задачу. Пусть к моменту времени $$ мы наблюдаем последовательность наград $$. Обозначим действие, принятое в момент времени $$ как $$ (индекс бандита, цвет кнопки). Также считаем, что каждый $$ сгенерирован независимо из некоторого распределения наград своего бандита $$, где $$ — это некоторый вектор параметров. В случае анализа кликов задача упрощается тем, что награда является бинарной $$, а вектор параметров — это просто параметры распределения Бернулли каждой вариации.

Тогда ожидаемой наградой бандита $$ будет $$. Если бы параметры распределений были известны, то мы легко бы вычислили ожидаемые награды и просто выбирали бы всегда вариант с максимальной наградой. Но, к сожалению, истинные параметры распределений нам неизвестны. Также обратим внимание, что в случае с кликами $$, а ожидаемая награда $$. В таком случае мы можем ввести априорное распределение на параметры распределения Бернулли и после каждого действия, наблюдая награду, сможем обновлять нашу «веру» в бандита $$, используя теорему Байеса. Для этого идеально подходит бета распределение по трем причинам:

• бета распределение является априорно сопряженным к распределению Бернулли, т.е. апостериорное распределение тоже имеет форму бета-распределения, но с другими параметрами:

• при $$ бета-распределение принимает форму равномерного распределения, т.е. именно такого, которое естественно использовать в ситуации полной неопределенности (например, в самом начале тестирования); чем более определенными становятся наши ожидания относительно прибыльности бандита, тем более скошенным становится распределение (влево — не прибыльный бандит, вправо — прибыльный);
• модель легко интерпретируема, $$ — это количество успешных испытаний, а $$ — количество неуспешных испытаний; среднее значение будет $$.

Посмотрим функции плотности для различных параметров бета-распределения:

support = np.linspace(0, 1, 1000)
fig, ax = plt.subplots()
for a, b in [(1, 1), (5, 5), (5, 10), (5, 25), (1, 7), (7, 1)]:
    ax.plot(support, stats.beta.pdf(support, a, b), 
            label='a=%i, b=%i' % (a, b))
ax.legend(loc='upper right', prop={'size': 20})
ax.set_title('Beta PDFs', fontsize=20)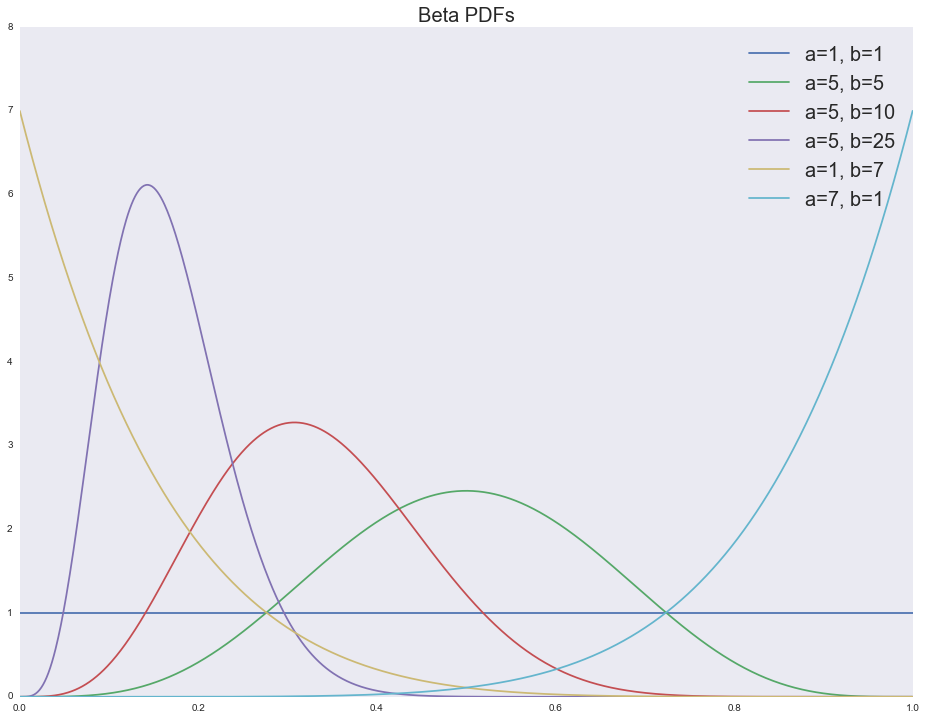

Получается, что имея некоторые априорные ожидания об истинном значении конверсии, мы можем использовать теорему Байеса и обновлять наши ожидания при поступлении новых данных. А форма априорного распределения после обновления ожиданий остается все тем же бета-распределением. Итак, у нас есть следующая модель:

Тут мы применяем вторую, вполне естественную эвристику: давайте будем для нового пользователя (новый эксперимент) семплировать руку бандита (вариацию кнопки) не случайно, а пропорционально нашим текущим ожиданиям о полезности этой руки. Но так как у нас байесовская постановка задачи, и мы не храним в явном виде наши оценки полезности, а храним распределение оценок полезности для каждой руки, то и алгоритм семплирования немного изменяется:

• Для всех бандитов введем два параметра бета-распределения и приравняем их к единице $$;
• повторяем в течении некоторого времени $$
  
  • для каждого бандита семплируем $$;
  • выбираем бандита с максимальной наградой $$;
  • используем $$-ого бандита в текущем эксперименте и получаем награду $$ (показываем ту кнопку текущему пользователю, которая по текущему семплу максимизирует награду);
  • обновляем параметры соответствующего априорного распределения (легко модифицируется для batch mode, если мы проводим не один, а серию экспериментов):
  • $$
    
  • $$
    

Семплирование Томпсона является эмпирикой, но для некоторых случаев доказаны теоремы асимптотической сходимости. В том числе и для Beta-Bernoulli случая, т.е. при $$ вероятность того, что бандиты с семплированием Томпсона сойдутся к верному решению, равна единице. Но это все теории, на практике нам важно следующее:

• если обозначить вероятность выигрыша на лучшем бандите за $$, то доля трафика, потраченного на эту опцию будет пропорциональна $$; в процессе обучения точность оценки будет возрастать, и доля трафика, потраченного на нужную опцию, будет расти;

• в любой момент времени у нас есть параметры распределения вероятностей выигрыша на каждой вариации (параметры бета-распределения), это позволяет нам применять всё те же тесты, что и при классическом тестировании;
• но отметим, что в отличие от тестов, мы не хотим получить ответ в виде статистической значимости разности кликов по разным вариациям, мы, как бизнес, хотим максимизировать CTR, а именно это и делает бандитская модель.

Эксперимент

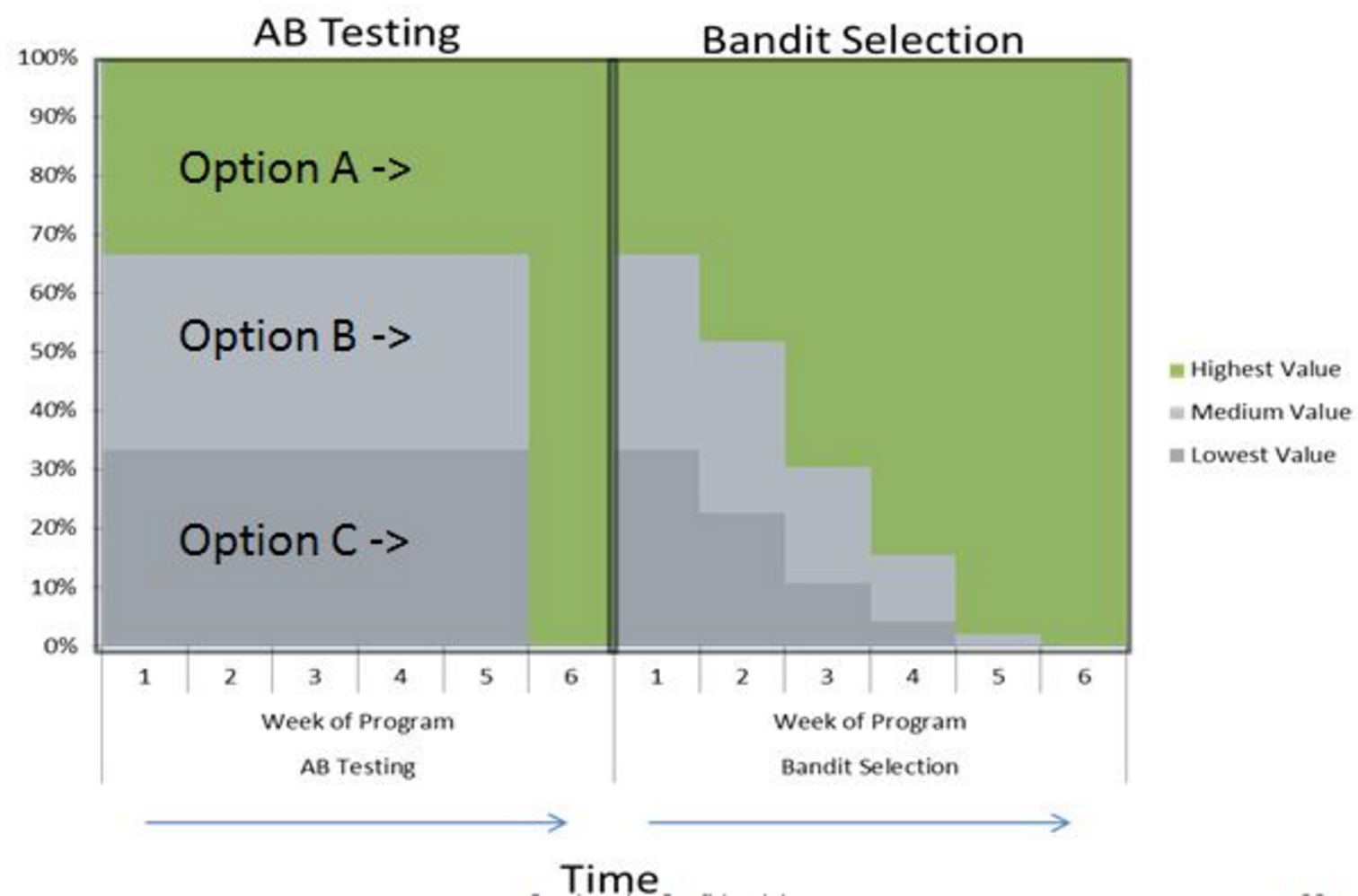
Проведем симуляционный эксперимент. Допустим, у нас всё те же пять вариаций кнопки, но со временем предпочтения пользователей нашего мурлычного сайта плавно меняются. В принципе, динамика уже сразу исключает применение одного A/B/n-теста, ну и ладушки.

# количество вариаций
n_variations = 5

# сколько раз меняются предпочтения
n_switches = 5

# каждые n_period_len показов кнопки предпочтения пользователей меняются
n_period_len = 2000

# истинные вероятности клика по каждой вариации
# напомню, что длина периода, в течение которого тренд не меняется, равна n_period_len
p_true_periods = np.array([
        [1, 2, 3, 4, 5],
        [2, 3, 4, 5, 1],
        [3, 4, 5, 2, 1],
        [4, 5, 3, 2, 1],
        [5, 4, 3, 2, 1]], dtype=np.float32).T**3
p_true_periods /= p_true_periods.sum(axis=0)

# отрисуем истинные вероятности
ax = sns.heatmap(p_true_periods)
ax.set(xlabel='Periods', ylabel='Variations', title='Probabilities of variations')
plt.show()

Теперь запустим симуляцию: будем выводить после каждого периода наши оценки вероятности клика по каждой вариации и убедимся, что к концу каждого периода находится оптимальная вариация. Также будем следить за тем, сколько трафика из n_period_len отправлено на каждую вариацию.

В первый период мы четко определяем победителя (самый правый график с явно выраженным пиком). Напоминаю, что каждый график на изображении — это распределение наших ожиданий относительно качества руки (конверсии вариации). Чем шире график, тем меньше неопределенности (прямая линия/равномерное распределение — это полная неопределенность); чем уже, тем больше неопределенности. Но вот во второй период мы уже приходим не с полной неопределенностью (равномерное распределение на параметры), а со статистикой, собранной в первый период, и потому мы видим, что существенная доля трафика уходит на старого победителя. К следующим периодам новым лучшим вариациям все труднее выходить в лидеры: обратите внимание, что дисперсия бывших лидеров (ширина пика) меняется очень медленно. Потому часто алгоритм не успевает сойтись за заданное количество шагов. Существует множество способов исправления этой ситуации, самым простым является постепенное выравнивание распределения (приведение к равномерному, т.е. со временем мы теряем уверенность в прошлых оценках — это вполне естественно). Запустим симуляцию без затухания и посмотрим на результаты после каждого периода.

x_support = np.linspace(0, 1, 1000)

alpha = dict([(i, [1]) for i in range(n_variations)])
beta = dict([(i, [1]) for i in range(n_variations)])

cmap = plt.get_cmap('jet')
colors = [cmap(i) for i in np.linspace(0, 1, n_variations)]

actionspp = []

for ix_period in range(p_true_periods.shape[1]):
    p_true = p_true_periods[:, ix_period]
    is_converged = False
    actions = []
    for ix_step in range(n_period_len):
        theta = dict([(i, np.random.beta(alpha[i][-1], beta[i][-1])) 
                      for i in range(n_variations)])
        k, theta_k = sorted(theta.items(), key=lambda t: t[1], reverse=True)[0]
        actions.append(k)

        x_k = np.random.binomial(1, p_true[k], size=1)[0]

        alpha[k].append(alpha[k][-1] + x_k)
        beta[k].append(beta[k][-1] + 1 - x_k)

    expected_reward = dict([(i, alpha[i][-1]/float(alpha[i][-1] + beta[i][-1])) 
                            for i in range(n_variations)])
    estimated_winner = sorted(expected_reward.items(), 
                              key=lambda t: t[1], 
                              reverse=True)[0][0]

    print 'Winner is %i' % i
    actions_loc = pd.Series(actions).value_counts()
    print actions_loc
    actionspp.append(actions_loc.to_dict())

    for i in range(n_variations):
        plt.axvline(x=p_true[i], color=colors[i], linestyle='--', 
                    alpha=0.3, label='true value of %i' % i)

        plt.plot(x_support, stats.beta.pdf(x_support, alpha[i][-1], beta[i][-1]), 
                 label='distribution of %i' % i, color=colors[i])
    plt.legend(prop={'size': 20})
    plt.title('Period %i; winner: true is %i, estimated is %i' % 
              (ix_period, 
               p_true.argmax(),
               estimated_winner),
              fontsize=20)
    plt.show()

actionspp = dict(enumerate(actionspp))

Период первый:

Winner is 4
4    1953
3      19
2      12
1       8
0       8
dtype: int64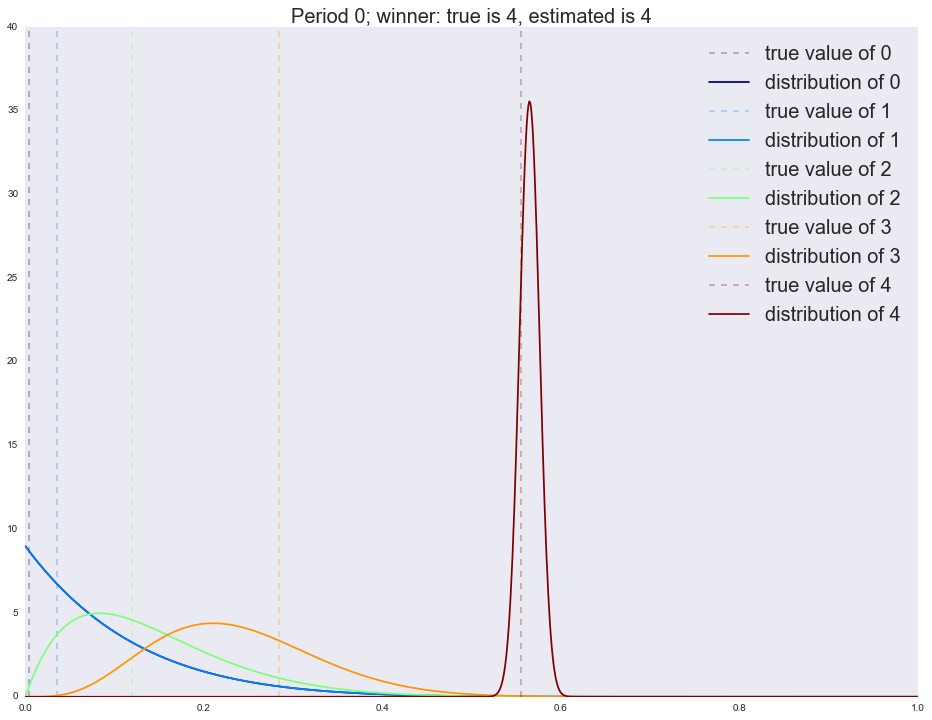

Период второй:

Winner is 4
3    1397
4     593
1       6
2       3
0       1
dtype: int64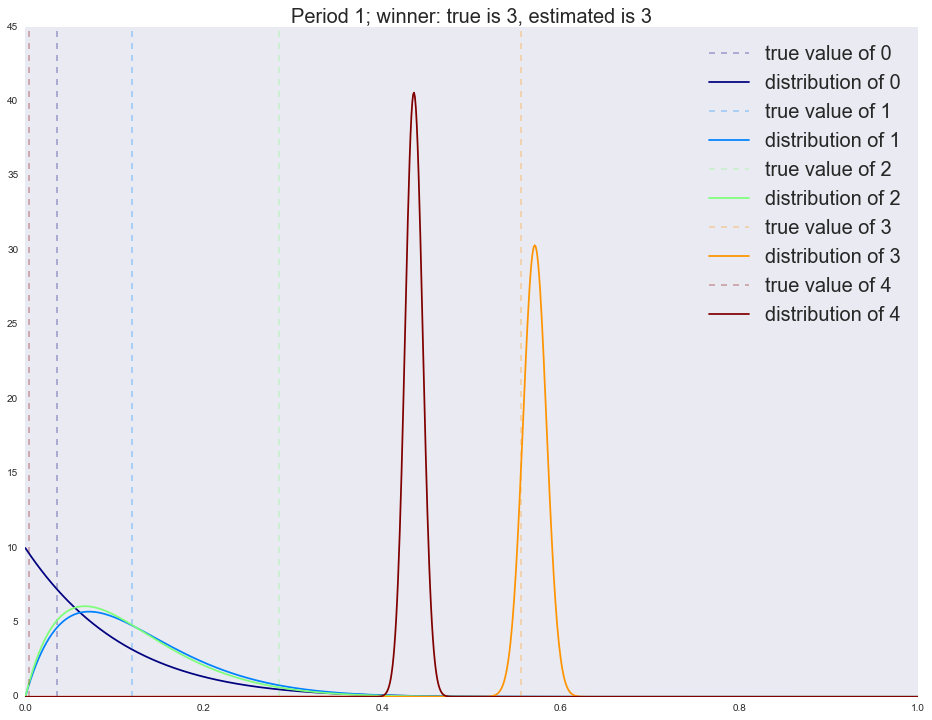

Период третий:

Winner is 4
2    1064
3     675
4     255
1       3
0       3
dtype: int64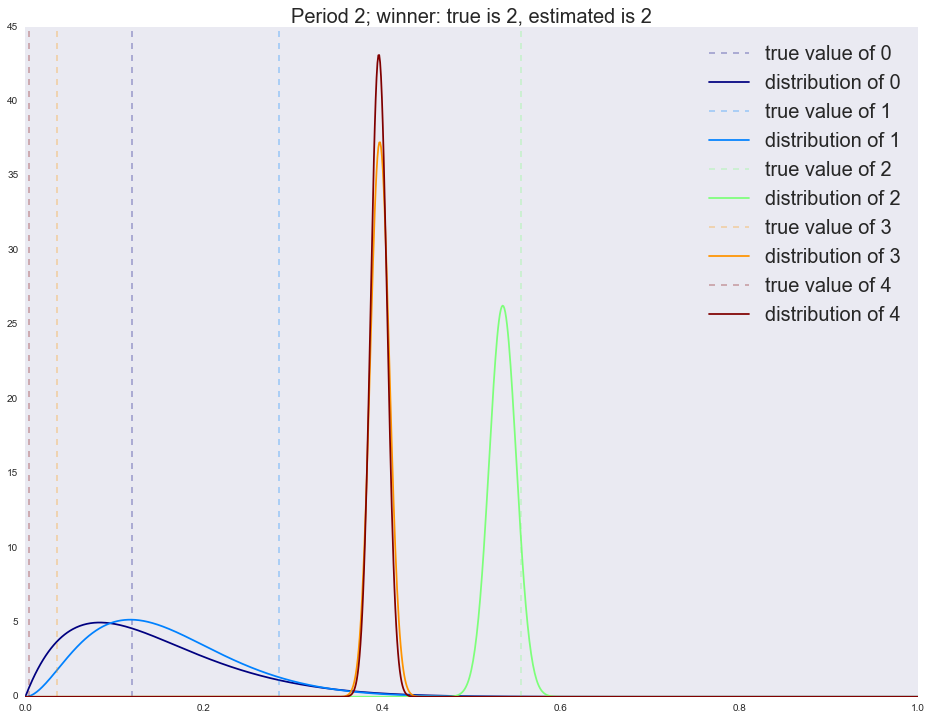

Период четвертый:

Winner is 4
1    983
2    695
4    144
3    134
0     44
dtype: int64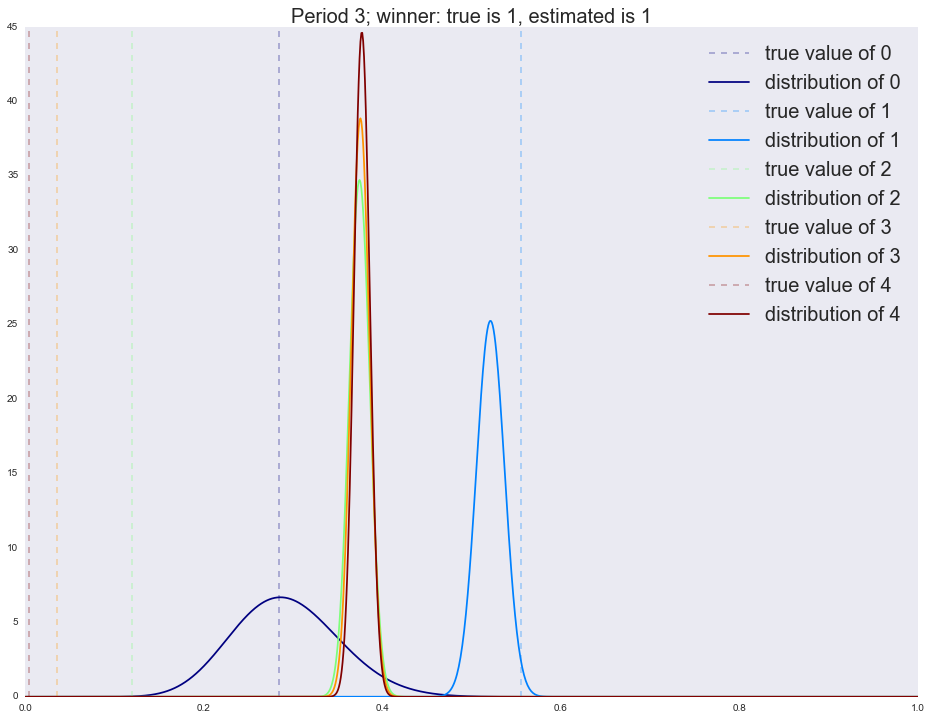

Период пятый:

Winner is 4
1    1109
0     888
4       2
2       1
dtype: int64

Отрисуем долю трафика, потраченного на каждую вариацию в каждый период.

df = []
for pid in actionspp.keys():
    for vid in actionspp[pid].keys():
        df.append({
                'Period': pid,
                'Variation': vid,
                'Probapility': actionspp[pid][vid]/1000.0
            })
df = pd.DataFrame(df)
ax = sns.barplot(x="Period", y="Probapility", hue="Variation", data=df)
ax.set(title="Ratio of traffic used for variations per period")
plt.show()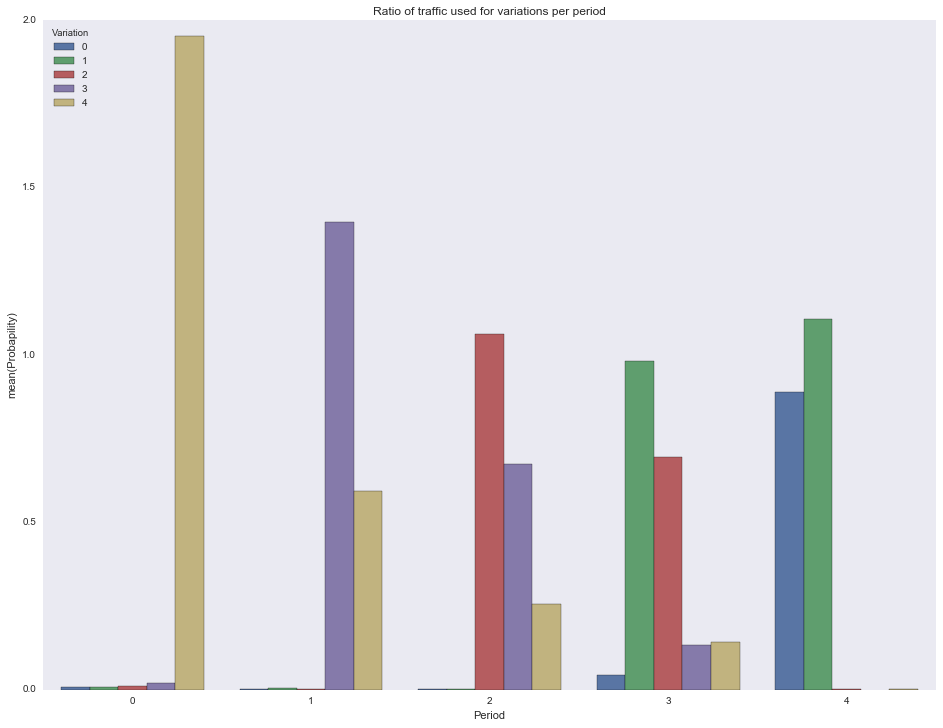

Ну и под конец нарисуем в динамике изменения наших ожиданий относительно крутости каждой вариации.

n_period_len = 3000

alpha = dict([(i, [1]) for i in range(n_variations)])
beta = dict([(i, [1]) for i in range(n_variations)])
decay = 0.99

plot_step = 25

for f in glob.glob("./../images/mab_gif/*.png"):
    os.remove(f)

img_ix = 0
height = 10 # 15
for ix_period in range(p_true_periods.shape[1]):
    p_true = p_true_periods[:, ix_period]
    is_converged = False
    actions = []
    for ix_step in tqdm_notebook(range(n_period_len)):
        if ix_step % plot_step == 0:
            expected_reward = dict([(i, alpha[i][-1]/float(alpha[i][-1] + beta[i][-1])) 
                                    for i in range(n_variations)])
            estimated_winner = sorted(expected_reward.items(), 
                                      key=lambda t: t[1], 
                                      reverse=True)[0][0]

            fig, ax = plt.subplots()
            ax.set_ylim(0, height)
            ax.set_xlim(0, 1)
            for i in range(n_variations):
                ax.axvline(x=p_true[i], color=colors[i], linestyle='--', 
                           alpha=0.3, label='true value of %i' % i)

                ax.plot(x_support, stats.beta.pdf(x_support, alpha[i][-1], beta[i][-1]), 
                        label='distribution of %i' % i, color=colors[i])
            ax.legend(prop={'size': 20})
            ax.set_title('Period %i, step %i; winner: true is %i, estimated is %i' % 
                         (ix_period, 
                          ix_step,
                          p_true.argmax(),
                          estimated_winner),
                         fontsize=20)

            fig.savefig('./../images/mab_gif/%i.png' % img_ix, dpi=80)
            img_ix += 1

            plt.close(fig)

            theta = dict([(i, np.random.beta(alpha[i][-1], beta[i][-1])) 
                          for i in range(n_variations)])
            k, theta_k = sorted(theta.items(), key=lambda t: t[1], reverse=True)[0]
            actions.append(k)

            x_k = np.random.binomial(1, p_true[k], size=1)[0]

            alpha[k].append(alpha[k][-1] + x_k)
            beta[k].append(beta[k][-1] + 1 - x_k)

            if decay > 0:
                for i in range(n_variations):
                    if i == k:
                        continue
                    alpha[i].append(max(1, alpha[i][-1]*decay))
                    beta[i].append(max(1, beta[i][-1]*decay))

print img_ix

for f in glob.glob("./../images/mab_gif/mab.gif"):
    os.remove(f)
!convert -delay 5 $(for i in $(seq 1 1 600); do echo ./../images/mab_gif/$i.png; done) -loop 0 ./../images/mab_gif/mab.gif
for f in glob.glob("./../images/mab_gif/*.png"):
    os.remove(f)

Результат без применения затухания (тяжелая гифка, 40мб)

Результат с применением затухания (тяжелая гифка, 40мб)

Заключение

В заключение, отметим еще несколько преимуществ бандитов для онлайн-экспериментов:

• бандиты позволяют добавлять новые вариации прямо в процессе эксперимента;
• если у вас есть некоторые априорные ожидания о том, что новая вариация лучше остальных, то вы можете добавить ее в эксперимент, изменив ожидания с равномерного распределения $$ на смещенное ожидание в сторону единицы $$;
• в случае, если варианты разнесены по инфраструктуре, и один из сервисов вышел из строя, то бандитская модель быстро это заметит и перестанет лить трафик в сломанную руку.

Самое главное: при использовании бандитов в разы увеличивается количество мурлыкающих котиков, разве это не прекрасно? Все остальные аргументы вообще ничего не стоят.

Спасибо Насте bauchgefuehl, Арсению arseny_info и Юре yorko за редактирование и советы.