news.shamcode.ru | «A/B-тест» в инженерно-геологических изысканиях на языке Python

«A/B-тест» в инженерно-геологических изысканиях на языке Python

воскресенье, 6 июня 2021 г. в 00:35:40

Python
Статистика в IT

1. Введение

При выполнении инженерно-геологических изысканий может возникнуть задача, связанная с сопоставлением данных полевых и лабораторных исследований на одних и тех же грунтах, с целью подтверждения корректной транспортировки проб от объекта изысканий до лаборатории (образцы не были деформированы и/или разрушены в ходе перевозки).

При данной постановке задачи можно применить методику A/B-тестирования со следующими параметрами:

Измеряемой метрикой будет среднее значение плотности скелета грунта (p_d, г/см³), характеризующее сложение проб. Данная величина имеет нормальный закон распределения;
Критерием проверки гипотезы будет служить t-критерий (критерий Стьюдента): для двух независимых выборок, если сопоставляемые полевые (до транспортировки) и лабораторные (после транспортировки) данные проводились на разных пробах грунта; для двух зависимых выборок, если исследования выполнены на одних и тех же пробах.

В рамках данной темы мы сгенерируем две случайные выборки, которые будем сопоставлять, сформулируем статистические гипотезы, проверим их и сделаем выводы.

2. Генерация выборок

2.1 Оценка объема выборок

В рамках дизайна эксперимента, перед генерацией выборок плотностей, прикинем их необходимый объем при заданном размере эффекта (ES - effect size), мощности (power) и допустимой ошибке I рода (α) (определения данных терминов приведено ниже). Расчет произведем с привлечением пакета statsmodels.

Размер эффекта (стандартизированный) – величина, характеризующая различие, которое мы хотим выявить, равная отношению разности средних значений по выборкам к взвешенному стандартному отклонению. В нашем случае:

${ES = \frac{{(\bar{X}_1 - \bar{X}_2)}_{obs}}{{S}_{pooled}}}$ ${ES = \frac{{(\bar{X}_1 - \bar{X}_2)}_{obs}}{{S}_{pooled}}}$

Взвешенное стандартное отклонение S_pooled для выборок одинакового размера можно расcчитать по формуле:

${S}_{pooled}= {\sqrt{\frac{{S}_{1}^2+{S}_{2}^2}{2}}}$

Существует условная классификация размера эффекта (Cohen, 1988) ES = 0.2 - маленький; 0.5 - средний; 0.8 - большой.

Мощность – вероятность не совершить ошибку II рода (обычно принимается равной 80%).

Пояснения по ошибкам I и II рода приведены в таблице ниже:

	H₀ верна	H₁ верна
H₀ принимается	H₀ верно принята	Ошибка II рода (β)
H₀ отвергается	Ошибка I рода (α)	H₀ верно отвергнута (power = 1-β)

Для описанных выше величин примем следующие значения:

α = 0.05 (вероятность выявить различия между средними при их отсутствии)
ES = 0.5 (размер эффекта составит половину от дисперсии измеряемых величин плотности).
Power = 0.8 (вероятность выявления установленного различия между средними значениями).

Теперь к коду:

#Импорт библиотек
import numpy as np
from statsmodels.stats.power import TTestIndPower

from matplotlib.pyplot import figure
import matplotlib.pyplot as plt

import scipy
from statsmodels.stats.weightstats import *

#Задаем параметры
effect = 0.5
alpha = 0.05
power = 0.8

analysis = TTestIndPower()

#Оценка размера выборки
size = analysis.solve_power(effect, power=power, alpha=alpha)

print(f'Размер выборки, шт.: {int(size)}')

Размер выборки, шт.: 63

При заданных значения мощности, размера эффекта и уровня значимости минимальный размер каждой выборки должен составлять 63 пробы. Для красоты округлим полученное число до 65 шт.

Давайте построим график зависимости необходимого размера выборок от размера эффекта при заданной мощности и уровне значимости.

plt.figure(figsize=(10, 7), dpi=80)

results = dict((i/10, analysis.solve_power(i/10, power=power, alpha=alpha)) 
               for i in range(2, 16, 1))

plt.plot(list(results.keys()), list(results.values()), 'bo-')

plt.grid()
plt.title('График зависимости необходимого объема выборки \n от размера эффекта')
plt.ylabel('Размер выборки n, шт.')
plt.xlabel('Размер эффекта ES, д.е.')

for x,y in zip(list(results.keys()),list(results.values())):

    label = "{:.0f}".format(y)

    plt.annotate(label, 
                 (x,y), 
                 textcoords="offset points", 
                 xytext=(0,10), 
                 ha='center')

plt.show()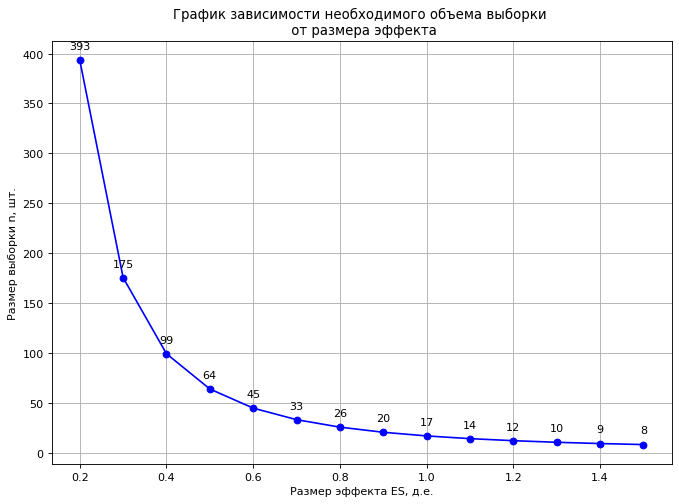

Данный график позволяет увидеть, как быстро изменяется необходимый объем выборок при уменьшении фиксируемого размера эффекта ES. Например: при выявлении различия в плотности проб грунта до и после их транспортировки в 0,03 г/см³ при стандартном отклонении в 0,1 г/cм³ (ES = 0,03 г/см³ / 0,1 г/см³ = 0,3 д.е.), необходимый объем проб по каждой выборке должен составить не менее 175 проб для заданной мощности и уровня значимости (power=0.80, α=0.05).

2.2 Генерация выборок

Теперь зная необходимый минимальный размер выборок, сгенерируем их с помощью библиотеки numpy.

Измеряемая физическая характеристика грунта (плотность скелета) имеет нормальный закон распределения. В рамках данного примера зададим генератору следующие значения среднего (X̄) и стандартного отклонения (S):

для первой выборки – X̄₁= 1,65 г/см³, S₁ = 0.15 г/см³;
для второй – X̄₂ = 1,60 г/см³, S₂ = 0.15 г/см³.

loc_1 = 1.65
sigma_1 = 0.15

loc_2 = 1.60
sigma_2 = 0.15

sample_size = 65
#Генерируем выборки с заданными параметрами
sample_1 = np.random.normal(loc=loc_1, scale=sigma_1, size=sample_size)
sample_2 = np.random.normal(loc=loc_2, scale=sigma_2, size=sample_size)

Постоим гистограммы и "ящик с усами" по полученным выборкам.

fig, axes = plt.subplots(ncols=2, figsize=(18, 5))

max_y = np.max(np.hstack([sample_1,sample_2]))
#Гистрограмма по выборке 1
count_1, bins_1, ignored_1 = axes[0].hist(sample_1, 10, density=True, 
                                          label="Выборка 1", edgecolor='black',
                                          linewidth=1.2)
axes[0].plot(bins_1, 1/(sigma_1 * np.sqrt(2 * np.pi)) *
               np.exp( - (bins_1 - loc_1)2 / (2 * sigma_12)),
         linewidth=2, color='r', label='плотность вероятности')
axes[0].legend()
axes[0].set_xlabel(u'Длина сессии, с')
axes[0].set_ylabel(u'Количество сессий, шт.')
axes[0].set_ylim([0, 5])
axes[0].set_xlim([1.1, 2.2])

#Гистрограмма по выборке 2
count_2, bins_2, ignored_2 = axes[1].hist(sample_2, 10, density=True, 
                                          label="Выборка 2", edgecolor='black', 
                                          linewidth=1.2, color="green")
axes[1].plot(bins_2, 1/(sigma_2 * np.sqrt(2 * np.pi)) *
               np.exp( - (bins_2 - loc_2)2 / (2 * sigma_22)),
         linewidth=2, color='r', label='плотность вероятности')
axes[1].legend()
axes[1].set_xlabel(u'Длина сессии, с')
axes[1].set_ylabel(u'Количество сессий, шт.')
axes[1].set_ylim([0, 5])
axes[1].set_xlim([1.1, 2.2])
plt.show()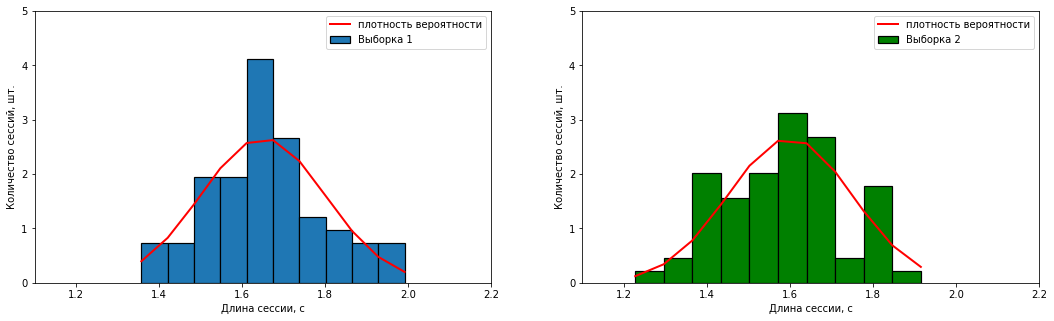

#Ящик с усами
fig, ax = plt.subplots(figsize=(8, 8))
axis = ax.boxplot([sample_1, sample_2], labels=['Выборка 1', 'Выборка 2'])

data = np.array([sample_1, sample_2])
means = np.mean(data, axis = 1)
stds = np.std(data, axis = 1)

for i, line in enumerate(axis['medians']):
    x, y = line.get_xydata()[1]
    text = ' μ={:.2f}\n σ={:.2f}'.format(means[i], stds[i])
    ax.annotate(text, xy=(x, y))

plt.ylabel('Плотность скелета грунта, г/см3')
plt.show()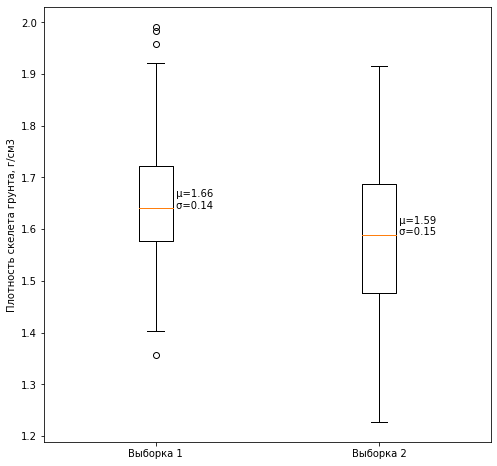

3. Формулировка гипотез

Пришло время для формулировки гипотез. У нас могут быть два случая:

Случай 1. Сопоставляемые полевые и лабораторные данные по определению плотности скелета грунта относятся к разным пробам, тогда t-критерий будет рассчитываться для двух независимых выборок;
Случай 2. Исследования в поле и лаборатории выполнены на одних и тех же пробах, тогда t-критерий будет рассчитываться для двух зависимых выборок.

Начнем с первого варианта.

Вариант 1. Для двух независимых выборок

С помощью двухвыборочного критерия Стьюдента проверим гипотезу о равенстве средних выборок.

Нулевая гипотеза H₀: средние значения равны μ1 = μ2.

Альтернативная гипотеза H₁: средние не равны μ₁≠μ₂.

Статистика:

$T({{X_1}^{n_1}},{{X_2}^{n_2}}) = \frac{\bar{X_1}-\bar{X_2}} {\sqrt{\frac{S_1^2}{n_1} + \frac{S_2^2}{n_2}}}$

Нулевое распределение: T(X₁ⁿ¹,X₂ⁿ²)≈~St(ν), где степень свободы ν вычисляется по следующей формуле

${\nu = \frac{ ({\frac{S_1^2}{n_1} + \frac{S_2^2}{n_2}})^2 } {\frac{S_1^4}{n_1^2(n_1-1)}+ \frac{S_2^4}{n_2^2(n_2-1)} } }$

Для расчета достигаемого уровня значимости воспользуемся методом ttest_ind модуля stats.

t_st, p_val = scipy.stats.ttest_ind(sample_1, sample_2, equal_var = False)
print(f't-критерий составил {round(t_st, 2)}')
print(f'Рассчитанный t-критерий дает достигаемый \
уровень значимости (p-value) равный {round(p_val, 3)}')

t-критерий составил 2.92

Рассчитанный t-критерий дает достигаемый уровень значимости (p-value) равный 0.004

Вывод для варианта № 1

Нулевая гипотеза H₀ о том, что средняя плотность скелета грунта не изменилась после транспортировки, отвергается на уровне значимости 0,05 (достигаемый уровень значимости p-value для сгенерированных выборок составил 0.004) в пользу альтернативной.

Давайте интервально оценим разность средних по данным выборкам.

c_m = CompareMeans(DescrStatsW(sample_1), DescrStatsW(sample_2))
print("95%% доверительный интервал: \
[%.4f, %.4f]" % c_m.tconfint_diff(usevar='unequal'))

95% доверительный интервал: [0.0235, 0.1228]

Так как ноль не попадает в рассматриваемый 95% доверительный интервал, мы можем сделать вывод, что средние значения рассматриваемых выборок отличаются на уровне значимости в 5%.

Вариант 2. Для двух связанных выборок

Допустим, что оценка плотности скелета грунта в полевых (до транспортировки) и лабораторных (после транспортировки) условиях проводилась для каждого образца. Тем самым выборки будут является зависимыми, а проверка нулевой гипотезы об отсутствии изменений в плотности грунта при транспортировке будет осуществляться с помощью двухвыборочного критерия Стьюдента для связанных выборок.

Нулевая гипотеза H₀: средние значения равны μ₁ = μ₂.

Альтернативная гипотеза H₁: средние не равны μ₁≠μ₂.

Статистика:

$T({{X_1}^{n}},{{X_2}^{n}}) = \frac{\bar{X_1}-\bar{X_2}} {\frac{S}{\sqrt{n}}}$ $S^2 = \frac{1}{n-1} \sum_{i=1}^n (D_i - \bar{D})^2, D_i = X_{1i} - X_{2i}$

Нулевое распределение: T(X₁ⁿ, X₂ⁿ) ~ St(n-1)

Для расчета достигаемого уровня значимости воспользуемся методом ttest_rel модуля stats.

t_st, p_val = stats.ttest_rel(sample_1, sample_2)
print(f't-критерий составил {round(t_st, 2)}')
print(f'Рассчитанный t-критерий дает достигаемый \
уровень значимости (p-value) равный {round(p_val, 3)}')

t-критерий составил 2.79

Рассчитанный t-критерий дает достигаемый уровень значимости (p-value) равный 0.007

Вывод для варианта № 2

Для наглядности также давайте интервально оценим разность средних по данным выборкам

print("95%% confidence interval: [%.4f, %.4f]"
      % DescrStatsW(sample_1 - sample_2).tconfint_mean())

95% confidence interval: [0.0208, 0.1255]

Так как ноль не попадает в рассматриваемый 95% доверительный интервал, мы можем сделать вывод, что средние значения рассматриваемых выборок отличаются.

5. Итог

В данной статье мы рассмотрели возможность применения языка Python при решении практической задачи в инженерной геологии, с попутным исследованием вопроса о необходимом объеме выборки для проверки гипотез.