javascript

9 алгоритмов сортировки и поиска для JS, о которых вас спросят на собеседовании

  • среда, 25 октября 2023 г. в 00:00:14
https://habr.com/ru/companies/simbirsoft/articles/769312/

Привет, Хабр!

Меня зовут Илья, я frontend-разработчик SimbirSoft. Долгое время вопрос изучения алгоритмов был холиварным. Со временем я убедился, что ни одно современное собеседование в крупную компанию не обходится без вопросов про алгоритмы, и в последний год их всё больше.

Даже если ты frontend-разработчик и решаешь прикладные задачи, тебе в любом случае придётся знать алгоритмы хотя бы на базовом уровне. Но статей на русском с объяснением алгоритмов и тем, как их реализовать на JavaScript, крайне мало. Поэтому хочу поделиться некоторыми алгоритмами сортировки и поиска, и немного рассказать про структуры данных. Знание алгоритмов и структур данных поможет вам в оптимизации приложений.

Статья будет полезна разработчикам любых направлений, которые начали свой путь к крепкому уровню middle.

Что такое алгоритмы?

Для начала давай разберёмся с базовыми определениями.

Алгоритм — набор инструкций описывающий порядок действий для достижения определённых целей или решения конкретных задач.

Из этого определения можно подметить такой факт, что любой код, который мы пишем, в той или иной степени является алгоритмом.

Структура данных — хранилище данных, устроенное максимально эффективным способом.

Алгоритмы и структуры данных неотделимы друг от друга, так как структуры данных — это информация, а алгоритмы — это инструкции по работе с этой информацией.

Пара слов о нотации Big O

Для измерения эффективности необходимо позвать на помощь арбитра, который сможет максимально критично оценить производительность алгоритма.

Big O — нотация, которая позволяет определить верхнюю границу скорости работы алгоритма. Как справедливо отметил один из комментаторов, это асимптотическая сложность, которая описывает верхнюю границу сложности алгоритма при увеличении размера входных данных, или то, как рост размера входных данных влияет на количество операций.

Чтобы было понятнее, рассмотрим на примере:

Обычный обход по массиву имеет сложность O(n), где n — количество элементов массива. Если внутри этого цикла добавить ещё один, который также будет проходить по всем элементам массива, то сложность внешнего цикла возрастёт до O(n2).

В Big O константы откидываются, представим ситуацию, что у нас существует функция, в которой существуют 2 одинаковых цикла.

const func = (arr) => {
    for(let i = 0; i < arr.length; i++) {
        ...
    }

    for(let j = 0; j < arr.length; j++) {
        ...
    }
}

Сложность её будет не O(2n) , как может вполне логично показаться, а O(n). Нотация Big O обращает внимание конкретно на число входных элементов — n, также на степени, логарифмы, факториалы и экспоненты этого числа.

Поначалу может показаться нелогичным, что функция с один циклом и функция с двумя циклами оцениваются по Big O как эквивалентные по временной сложности, но хочу подчеркнуть — Big O нотация показывает зависимость алгоритма от входных данных. Именно поэтому Big O не гарантирует, что алгоритм O(1) будет самым быстрым, но даёт понять, что скорость работы этого алгоритма не будет зависеть от входных данных.

Немного про структуры данных

Поговорим немного о тех структурах данных, которые будем использовать дальше в ходе статьи.

Граф. Структура данных, состоящая из «вершин» и «ребёр». Вершины имеют значение, именуемое «вес», рёбра соединяют вершины друг с другом. Получается своего рода сущность в виде сетки. Графом можно наглядно описать любые взаимосвязи в природе.

Пример неориентированного, невзвешенного графа
Пример неориентированного, невзвешенного графа
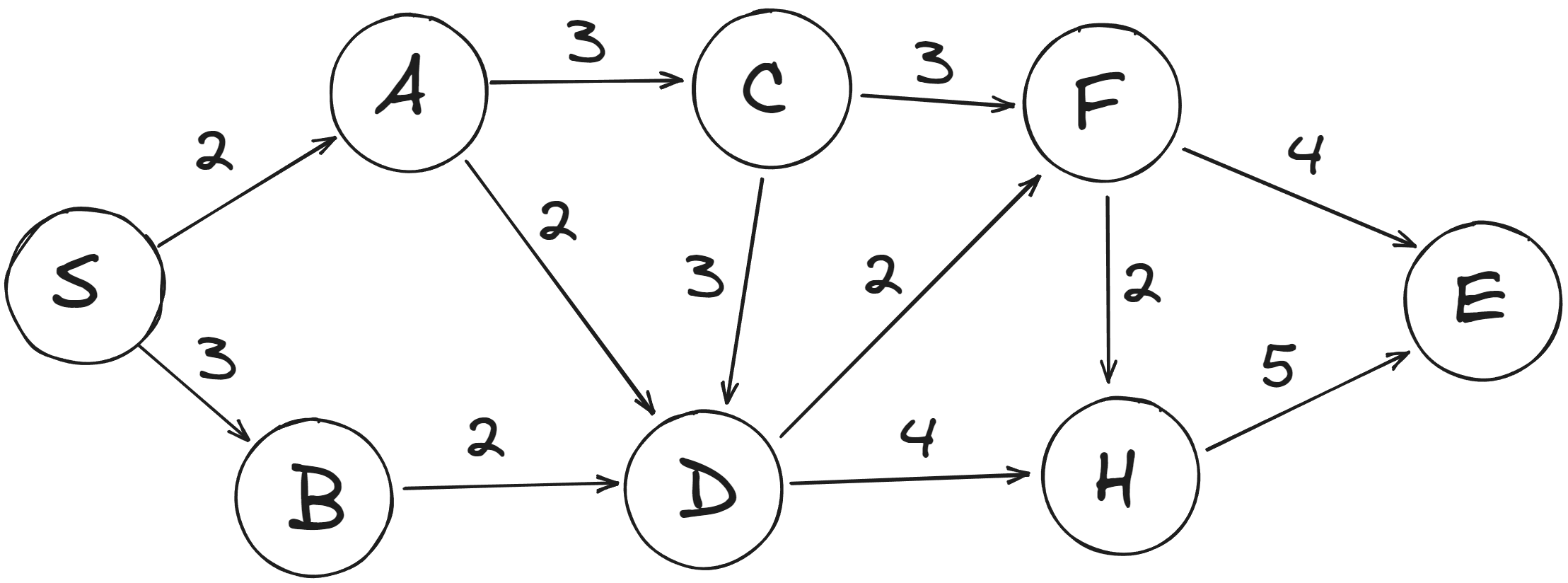
Пример ориентированного, взвешенного графа
Пример ориентированного, взвешенного графа

Дерево. При тщательном рассмотрении может показаться, что дерево очень похоже на граф, и так оно и есть. Это структура данных, представляющая собой связанный граф, не имеющий циклов.

Стек. Базовая структура данных, в которой реализовано только добавление и удаление элементов. Данные в этой структуре организованы по принципу LIFO (Last In First Out) «Последним зашёл, первым вышел». Такой способ организации можно сравнить со стопкой тарелок.

Очередь. Структура данных, название которой говорит само за себя. В ней также реализованы лишь методы добавления и удаления элементов. В этой структуре данные организованы по принципу FIFO (First In First Out) «Первым зашёл, первым вышел». Яркий пример — очередь в магазине.

Понимание вышеописанных структур данных даст нам понимание работы алгоритмов, которые на первый взгляд кажутся сложными и тяжёлыми к восприятию.

Алгоритмы сортировки

Переходим к разговору об алгоритмах сортировки. В этом разделе вы узнаете про такие алгоритмы, как:

  • Сортировка пузырьком;

  • Сортировка выбором;

  • Циклическая сортировка;

  • Быстрая сортировка;

Рассмотрим, чем они отличаются друг от друга, для чего применяются и где используются. Также мы рассмотрим на их имплементацию и визуализацию, и разберёмся, как реализовать их шаг за шагом.

Перед тем, как перейдём к изучению алгоритмов сортировки, надо уточнить, что алгоритмы сортировки подразделяют на стабильные и нестабильные.

Алгоритм является стабильным только в том случае, если он не меняет порядок элементов с одинаковыми значениями относительно друг друга. Соответственно, нестабильный алгоритм — наоборот.

При сортировки списка чисел на этот параметр можно не обращать внимания, а если мы собираемся сортировать массив/объект данных, то этот показатель может сыграть злую шутку.

Например, существует такой список:

const users = [
	{ number: 4, name: "Николай" },
	{ number: 2, name: "Анастасия" },
	{ number: 1, name: "Тимур" },
	{ number: 2, name: "Евгений" },
	{ number: 3, name: "Катерина" }
]

После сортировки стабильным алгоритмом этот список будет выглядеть следующим образом:

const users = [
	{ number: 1, name: "Тимур" },
	{ number: 2, name: "Анастасия" },
	{ number: 2, name: "Евгений" },
	{ number: 3, name: "Катерина" }
	{ number: 4, name: "Николай" }
]

Пользователь «Анастасия» гарантированно будет находиться выше пользователя «Евгений», так как это было в исходном массиве. Нестабильный алгоритм гарантировать это не может.

Сортировка пузырьком

Сортировка пузырьком — самый примитивный и базовый алгоритм сортировки. Он является основой для некоторых других алгоритмов. Этот алгоритм является стабильным. Сортировка пузырьком перебирает весь массив элементов, сравнивая два соседних элемента друг с другом и меняя их местами в соответствии с условиями. Элементы с большим значением опускаются вниз массива, а элементы с наименьшим значением поднимаются вверх, подобно пузырькам газа.

Сложность алгоритма: O(n2), где n — количество элементов массива. Так как мы запускаем вложенный цикл, сложность алгоритма равна O(n2)

Шаги реализации:

  1. Запускаем цикл i по массиву.

  2. Запускаем внутренний цикл j, который идёт от 0 до arr.length - i. Это ускоряет алгоритм, так как он не проходит по уже отсортированным элементам.

  3. Во внутреннем цикле проверяем соседние элементы и меняем их местами, если сосед слева больше соседа справа.

Визуализация:

Пример кода:

const bubbleSort = (arr) => {
  for (let i = 0; i < arr.length; i++) {
    for (let j = 0; j < arr.length - i; j++) {
      if (arr[j] > arr[j + 1]) {
        [arr[j], arr[j + 1]] = [arr[j + 1], arr[j]]; // Меняем значения переменных
      }
    }
  }
};

Алгоритм следует использовать в следующем случае:

  • Когда количество входных данных невелико, так как его временная сложность составляет O(n2).

Задачи для тренировки:

Сортировка выбором

Этот алгоритм сортировки при каждой итерации проходит по неотсортированной части массива, находит минимальный элемент и переносит его в начало массива.

Может быть как стабильным, так и нестабильным алгоритмом, в зависимости от реализации. В данном примере приведена стабильная реализация.

Сложность алгоритма: O(n2).

Шаги реализации:

  1. Запускаем цикл i по массиву.

  2. Внутри цикла создаём переменную, равную итерации цикла max = i.

  3. Запускаем внутренний цикл j по оставшимся элементам массива до его конца.

  4. Если элемент arr[max] > arr[j], то присваиваем max значение j.

  5. По окончании внутреннего цикла j переменная max хранит индекс наименьшего неотсортированного элемента массива.

  6. Меняем местами элементы с индексами i и max.

Визуализация:

Пример кода: 

const selectedSort = (arr) => {
  for (let i = 0; i < arr.length; i++) {
    let min = i;

    for (let j = i + 1; j < arr.length; j++) {
      if (arr[min] > arr[j]) {
        min = j; // Меняем значение переменной на наибольшее значение
      }
    }

    [arr[i], arr[max]] = [arr[max], arr[i]]; // Меняем значения переменных
  }
};

Алгоритм следует использовать в следующем случае:

  • Когда количество входных данных невелико, так как его временная сложность составляет O(n2).

Задачи для тренировки:

Циклическая сортировка

Основной идеей алгоритма циклической сортировки является разложение массива на циклы. Затем, внутри этих циклов происходят перестановки элементов до тех пор, пока все циклы не завершатся и массив не будет отсортирован.

Алгоритм циклической сортировки является нестабильным.

Хотя алгоритм циклической сортировки не является простым в понимании, он ценится за то, что изменения элементов массива происходят только тогда, когда элемент ставится на своё место. Это особенно важно, если изменение элементов массива является затратным.

Очень хорошее видео, которое поможет понять работу этого алгоритма

Сложность алгоритма: O(n2).

Шаги реализации:

  1. Запускаем цикл i, который должен пройти по всему массиву.

  2. Создаём временную переменную position, которая будет равна i.

  3. Запускаем внутренний цикл j, который перебирает всех соседей справа.

  4. Когда внутри цикла j находим элемент, который меньше arr[i], увеличиваем position на единицу.

  5. Если значение position равно i, переходим к следующей итерации внешнего цикла i.

  6. Пропускаем дубликаты, сравнивая значения элементов под индексами position и i с помощью цикла.

  7. Меняем местами элементы под индексами i и position.

  8. Запускаем цикл, пока position не будет ссылаться на i.

  9. Повторяем все операции, описанные внутри цикла j.

Визуализация

Пример кода:

function cycleSort(arr) {
  for (let i = 0; i < arr.length; i++) {
    let value = arr[i];
    let position = i;

    for (let j = i + 1; j < arr.length; j++) {
      if (arr[j] < value) {
        position++;
      }
    }
    if (position === i) {
      continue;
    }
    while (value === arr[position]) { // Избавляемся от дубликатов
      position++;
    }

    [arr[position], value] = [value, arr[position]]; // Меняем значения переменных

    while (position !== i) { // Запускаем цикл в обратную сторону
      position = i;
      for (let k = i + 1; k < arr.length; k++) {
        if (arr[k] < value) {
          position++;
        }
      }
      while (value === arr[position]) { // Избавляемся от дубликатов
        position++;
      }
      [arr[position], value] = [value, arr[position]]; // Меняем значения пременных
    }
  }
  return arr;
}

Алгоритм следует использовать в следующем случае:

  • Когда требуется минимальное количество перестановок в массиве.

Задачи для тренировки:

Быстрая сортировка

Алгоритм быстрой сортировки работает следующим образом: он определяет так называемый «‎стержень» и разбивает массив на подмассивы относительно «‎стержня», которые затем сортируются.

Этот алгоритм сортировки является нестабильным.

Сложность алгоритма в среднем: O(n * log n).

Сложность алгоритма в худшем случае: O(n2).

Шаги реализации:

  1. Поскольку реализация рекурсивная, вначале устанавливаем условие выхода из рекурсии: если входной массив имеет длину меньше 2, возвращаем массив.

  2. Создаем переменную pivot, которая ссылается на случайный элемент в массиве.

  3. Создаем массив с большими значениями, в котором будут храниться элементы больше pivot.

  4. Также создаем массив с наименьшими значениями, в котором будут храниться элементы меньше pivot.

  5. Запускаем цикл по массиву i, в котором сравниваем текущий элемент с pivot и помещаем его либо в массив с большими значениями, либо в массив с меньшими значениями.

  6. Возвращаем массив, состоящий из объединения массивов с меньшими и большими значениями, а между ними помещаем pivot.

Визуализация:

Пример кода:

const qsort = (arr) => {
  if (arr.length <= 1) {
    return arr
  }

  const pivot = arr[Math.floor(Math.random() * arr.length)]
  const greater = []
  const less = []

  for (let i = 0; i < arr.length; i++) {
    if (arr[i] > pivot) {
      greater.push(arr[i])
    }

    if (arr[i] < pivot) {
      less.push(arr[i])
    }
  }

  return [...qsort(less), pivot, ...qsort(greater)]
}

Алгоритм следует использовать в следующих случаях:

  • При обработке большого объема входных данных.

  • Когда требуется использовать наиболее быстрый алгоритм (в среднем этот алгоритм быстрее, чем рассмотренные ранее, но необходимо учитывать возможные негативные сценарии).

Задачи для тренировки:

Алгоритмы поиска

Переходим к разговору об алгоритмах поиска. В этом разделе вы узнаете про такие алгоритмы, как:

  • Линейный поиск

  • Бинарный поиск

  • Поиск в ширину и глубину

  • Алгоритм Дейкстры

Аналогично алгоритмам сортировки рассмотрим их имплементацию и визуализацию, также разберём, для чего они были придуманы, как и где применяются.

Линейный поиск

Линейный поиск — это самый примитивный алгоритм поиска, который работает как с отсортированными, так и с не отсортированными массивами.

Сложность алгоритма: О(n).

Шаги реализации:

  1. Запускаем цикл по массиву i.

  2. Проверяем текущий элемент на соответствие искомому элементу, в случае не соответствия идём дальше. Если элемент соответствует искомому, возвращаем его индекс.

  3. Если элемента нет в массиве, возвращаем -1.

Пример кода:

const linearSearch = (arr, findEl) => {
	for (let i = 0; i < arr.length; i++) {
		if (arr[i] === findEl) {	
			return i
		}
	}
	return -1
}

Алгоритм следует использовать в следующих случаях:

  • Когда массив входных данных невелик.

  • Когда мы можем пожертвовать производительностью в угоду простоты реализации.

Задачи для тренировки:

Бинарный поиск

Основная идея бинарного поиска заключается в делении массива по полам и отсеивании не подходящей части. Алгоритм имеет смысл использовать только с отсортированными массивами.

Сложность алгоритма в лучшем случае: O(1).

Сложность алгоритма в среднем: O(logn).

Шаги реализации:

  1. Создаём два указателя на начало массива и конец массива.

  2. Запускаем цикл, который итерируется до тех пор, пока указатель на начало не совпадает с указателем на конец массива.

  3. Внутри цикла создаём указатель на середину массива.

  4. Проверяем, если элемент по середине равен искомому элементу, возвращаем его индекс.

  5. Если средний элемент меньше искомого элемента, тогда указатель на начало смещаем на mid + 1. Иначе указатель на конец смещаем на mid - 1.

  6. В случае если искомого элемента в массиве нет, возвращаем -1.

Пример кода: 

const binarySearch = (arr, findItem) => {
  let start = 0;
  let end = arr.length - 1;

  while (start <= end) {
    let mid = Math.floor((start + end) / 2);

    if (arr[mid] === findItem) {
      return mid;
    }

    if (arr[mid] < findItem) {
      start = mid + 1; // Отбрасываем левую часть массива
    } else {
      end = mid - 1; // Отбрасываем правую часть массива
    }
  }

  return -1;
};

Алгоритм следует использовать в следующих случаях:

  • Когда входящий массив отсортирован.

  • Когда нам необходимо максимально производительное решение.

Задачи для тренировки:

Поиск в глубину (Depth-First Search)

Поиск в глубину — это алгоритм обхода или поиска в таких структурах данных, как деревья или графы. Основан на такой структуре данных, как стек. Алгоритм начинает работу с корневого узла (в случае графа в качестве корневого узла выбирается какой-либо произвольный узел) и прежде чем вернуться назад, проходит как можно дальше по каждой ветви.

Сложность алгоритма: O(V + E).

Шаги реализации:

  1. В случае обхода графа необходимо проинициализировать объект visited, который будет хранить вершины, которые прошёл алгоритм во избежание попадания в бесконечный цикл. В случае обхода по дереву этот шаг можно пропустить.

  2. Создаём массив stack, который будет исполнять роль стека, сразу заполняем его значением вершины, с которой начнём обход.

  3. Запускаем цикл, который будет итерироваться до тех пор, пока стек не опустеет.

  4. Достаём первое значение из стека и помещаем его в переменную vert.

  5. Проверяем, имеет ли эта вершина дочерние вершины.

  6. В случае если дочерние вершины найдены, добавляем их в начало стека.

  7. В случае обхода графа запускаем цикл, который будет проходить по дочерним вершинам, и если они не были пройдены алгоритмом ранее, класть их в стек.

Визуализация:

Пример кода в дереве: 

const dfs = (tree, start) => {
  const stack = [start];

  while (stack.length > 0) {
    const vert = stack.shift(); // Выбираем первую вершину из стека

    if (tree[vert]) {
      stack.unshift(...tree[vert]); // Добавляем вершины в начало стека
    }
  }
};

Пример кода в графе:

const dfs = (graph, start) => {
  const visited = {};
  const stack = [start];

  while (stack.length !== 0) {
    const vert = stack.shift(); // Выбираем первую вершину из стека

    if (!visited[vert]) {
      visited[vert] = true; // Отмечаем вершину как пройденую, если ранее не проходили её
    }

    if (graph[vert]) {
      for (let subVert of graph[vert]) {
        if (!visited[subVert]) {
          stack.unshift(subVert); // Добавляем вершину в начало стека
        }
      }
    }
  }
};

Алгоритм следует использовать в следующих случаях:

  • Когда мы знаем, что искомая вершина находится дальше всего от стартовой, или если граф имеет большую ширину.

  • Когда нам необходимо найти пути между вершинами.

Задачи для тренировки:

Поиск в ширину (Breadth-First Search)

Алгоритм поиска в ширину очень похож на описанный выше алгоритм поиска в глубину, отличается лишь тем, что в начале проходит все соседние узлы начальной вершины, потом все соседние узлы соседних вершин, и так далее, пока не пройдёт весь граф или не найдёт искомую вершину. Ещё одно отличие заключается в том, что основан этот алгоритм на такой структуре данных, как очередь.

Сложность алгоритма: O(V + E).

Шаги реализации:

  1. В случае обхода графа создаём объект visited, который будет хранить в себе информацию о пройденных вершинах, чтобы избежать бесконечного цикла.

  2. Создаём массив queue, который будет исполнять роль очереди.

  3. Запускаем цикл, который будет итерироваться до тех пор, пока очередь не опустеет.

  4. Достаём первый элемент из очереди и помещаем его в переменную vert.

  5. Проверяем, имеет ли эта вершина дочерние вершины.

  6. Если дочерние вершины имеются, добавляем их в конец очереди.

  7. В случае обхода графа запускаем цикл, который будет проходить по дочерним вершинам текущей вершины vert, и если алгоритм не проходил их ранее, добавляем их в конец очереди.

Визуализация:

Пример кода в дереве: 

const bfs = (tree, start) => {
  const queue = [start];

  while (queue.length !== 0) {
    const vert = queue.shift(); // Выбираем первую вершину из очереди

    if (tree[vert]) {
      queue.push(...tree[vert]); // Добавляем вершины в конец очереди
    }
  }
};

Пример кода в графе:

const bfs = (graph, start) => {
  const visited = {};
  const queue = [start];

  while (queue.length !== 0) {
    const vert = queue.shift(); // Выбираем первую вершину из очереди

    if (!visited[vert]) {
      visited[vert] = true; // Отмечаем вершину как пройденую, если ранее не проходили её
    }

    if (graph[vert]) {
      for (let subVert of graph[vert]) {
        if (!visited[subVert]) {
          queue.push(subVert); // Добавляем вершину в конец очереди
        }
      }
    }
  }
};

Алгоритм следует использовать в следующих случаях:

  • Когда мы знаем, что искомая вершина находится близко к стартовой, или если граф имеет большую глубину.

  • Когда нам необходимо найти кратчайшее расстояние в невзвешенном графе.

Задачи для тренировки:

Алгоритм Дейкстры

Основная идея алгоритма — создание дерева кратчайших путей с заданным источником в качестве корня. Алгоритм Дейкстры — один из самых популярных алгоритмов для нахождения короткого пути в взвешенном графе. Незаменим в работе GPS-навигации.

Сложность алгоритма: O(V)

Шаги реализации:

  1. Создаём объект parents, который будет хранить историю переходов по графу, объект costs , который будет хранить стоимости переходов, массив queue — очередь обхода вершин.

  2. Запускаем цикл, который проходит по вершинам графа и заполняет стартовыми значениями объект стоимости и очередь.

  3. Стоимость перехода в стартовую вершину равна 0, для остальных вершин Infinity.

  4. Запускаем цикл по очереди, находим элемент с наименьшей стоимостью перехода и помещаем её в переменную.

  5. Если элемент с наименьшей стоимостью существует и значение перехода в него не равно Infinity, запускаем цикл по дочерним вершинам.

  6. Находим новую стоимость, складывая стоимость перехода в родительскую и дочернюю вершину.

  7. Если стоимость перехода в дочернюю вершину больше новой стоимости, то обновляем стоимость для дочерней вершины в объекте стоимости, в истории переходов для дочерней вершины устанавливаем значение родительской вершины и добавляем дочернюю вершину с новой стоимостью в конец очереди.

  8. Повторяем шаги 4-7, пока очередь не опустеет.

Визуализация:

Пример кода:

const getLowestCostNode = (queue) => {
  let min = Infinity;
  let lowIndex;

  for (let i = 0; i < queue.length; i++) {
    const [, value] = queue[i];
    if (value < min) {
      min = value;
      lowIndex = i;
    }
  }

  const lowestNode = queue.splice(lowIndex, 1)[0];
  return lowestNode;
};

const dijkstra = (graph, start) => {
  const parents = {};
  const costs = {};
  const queue = [];

  for (let vert in graph) {
    if (vert === start) {
      costs[vert] = 0;
      queue.push([vert, 0]);
    } else {
      costs[vert] = Infinity;
      queue.push([vert, Infinity]);
    }
    parents[vert] = null;
  }

  while (queue.length) {
    const node = getLowestCostNode(queue);
    let [vert, value] = node;
    const cost = costs[vert];

    if (node || value !== Infinity) {
      for (let subNode in graph[vert]) {
        const nextSubNodeValue = graph[vert][subNode];
        const newCost = cost + nextSubNodeValue;
          if (costs[subNode] > newCost) {
            costs[subNode] = newCost;
            parents[subNode] = vert;
            queue.push([subNode, newCost]);
          }
      }
    }
  }
};

Алгоритм следует использовать в следующих случаях:

  • Когда необходимо найти кратчайший путь в взвешенном графе.

  • Когда граф не имеет отрицательных весов.

Задачи для тренировки:

Подводим итоги

Алгоритмы, которые мы с вами рассмотрели, являются базовыми, их должен знать каждый разработчик. Возможно, они не всем пригодятся в повседневной работе, но тем не менее знать и понимать, как они работают, просто необходимо.

Мир алгоритмов очень большой и насыщенный, существует огромное множество различных алгоритмов, каждый из которых решает какую-то конкретную задачу в определённой среде.

Спасибо что дочитали до конца. Буду благодарен, если поделитесь этой статьей с коллегами. Пишите в комментариях, о работе каких ещё алгоритмов вам было бы интересно узнать! Всем приятной работы/учёбы, и не забывайте, что алгоритмы окружают нас :)

Использованные источники:

Спасибо за внимание!

Больше авторских материалов для frontend-разработчиков от моих коллег читайте в соцсетях SimbirSoft – ВКонтакте и Telegram.