5 известных нерешённых задач, условие которых нетрудно понять
- четверг, 2 ноября 2023 г. в 00:00:22
В этой статье я расскажу вам про 5 моих любимых нерёшенных задач, условие которых очень легко понять, однако очень трудно решить.
Эти задачи показались мне интересными, поэтому я решил написать про них статью. И нет, здесь не будет их доказательств.
Верно ли, что каждое чётное число, большее 2, можно представить в виде суммы двух простых чисел?
Это очень известная гипотеза, которая, однако, пока не решена.
Нам известно, что любое чётное число можно представить в виде 4 простых чисел, а любое нечётное - в виде трёх (см. Тернарная проблема Гольдбаха). Также эта гипотеза верна для всех чётных чисел, не превышающих
Доказано, что любое достаточно большое чётное число можно представить в виде суммы простого и полупростого числа (полупростое число - это произведение двух простых чисел).
Чем больше наше чётное число, тем, очевидно, больше вероятность, что его можно представить в виде суммы 2-х простых чисел. Ещё я написал небольшую программку, которая должна проверять гипотезу.
#include <iostream>
#include <vector>
#include <algorithm>
// Программа проверяет справедливость гипотезы от 4 до х
int main() {
long long x = 1000000;
char arr[x];
std::vector<long> a = {};
arr[0] = '0';
arr[1] = '0';
for (long long i = 2; i < x; i++) arr[i] = '1';
long long s = 1;
for (long long i = 0; i < x; i++) {
if (arr[i] == '0') continue;
a.push_back(i);
for (long long j = i*i; j < x; j = j + i) arr[j] = '0';
}
for (long long i = 4; i < x; i+=2) {
for (long n:a) {
if (std::find(a.begin(), a.end(), i-n) != a.end()) {
if (n > 100) std::cout<<i<<"="<<n<<"+"<<i-n<<std::endl;
break;
}
}
}
};Если , где
натуральные числа и
, то
имеют общий делитель.
За доказательство или опровержение этой гипотезы американский миллиардер Эндрю Бил положил приз в один миллион долларов.
Существует множество примеров решения этого уравнения, однако для них всех имеют общий делитель, например,
.
Гипотеза Била является обобщением Великой теоремы Ферма. Действительно, если гипотеза Била справедлива, и существуют такие наименьшие числа , что
, то, поскольку
имеют общий делитель, верно также и
, где
- это общий делитель трёх чисел. Но наши числа
не наименьшее, и мы пришли к противоречию.
То есть, если гипотеза Била справедлива, то тогда автоматически справедлива и Великая теорема Ферма, кстати говоря, доказанная в 1995 году.
На 2013 год гипотеза была проверена для случаев, когда все 6 чисел не превышают 1000.
Также справедливость гипотезы Била доказана при значениях , равных
, где
- любое натуральное число.
Верно ли, что простых чисел-близнецов бесконечно много?
Простые числа-близнецы - это простые числа, разница между которыми равна 2. Например, числа 29 и 31 являются простыми числами-близнецами.
Доказано, что существует бесконечно много простых чисел, разница между которыми меньше, чем 246. Однако до двойки всё ещё далеко..
Самые большие известные простые числа-близнецы - это . Такое огромное число говорит в пользу гипотезы. Однако всё необходимо доказывать строго.
Известно, что если ряд ,где
- это k-тое простое число, сходится, то тогда гипотеза неверна.
Между прочим, иногда очень трудно понять, сходится ряд или расходится. Например, ряд расходится, однако даже если учесть все известные науке простые числа, сумма их обратных дробей (1/p) будет меньше четырёх!
Существуют ли такие натуральные числа ,для которых
и
являются квадратами натуральных чисел?
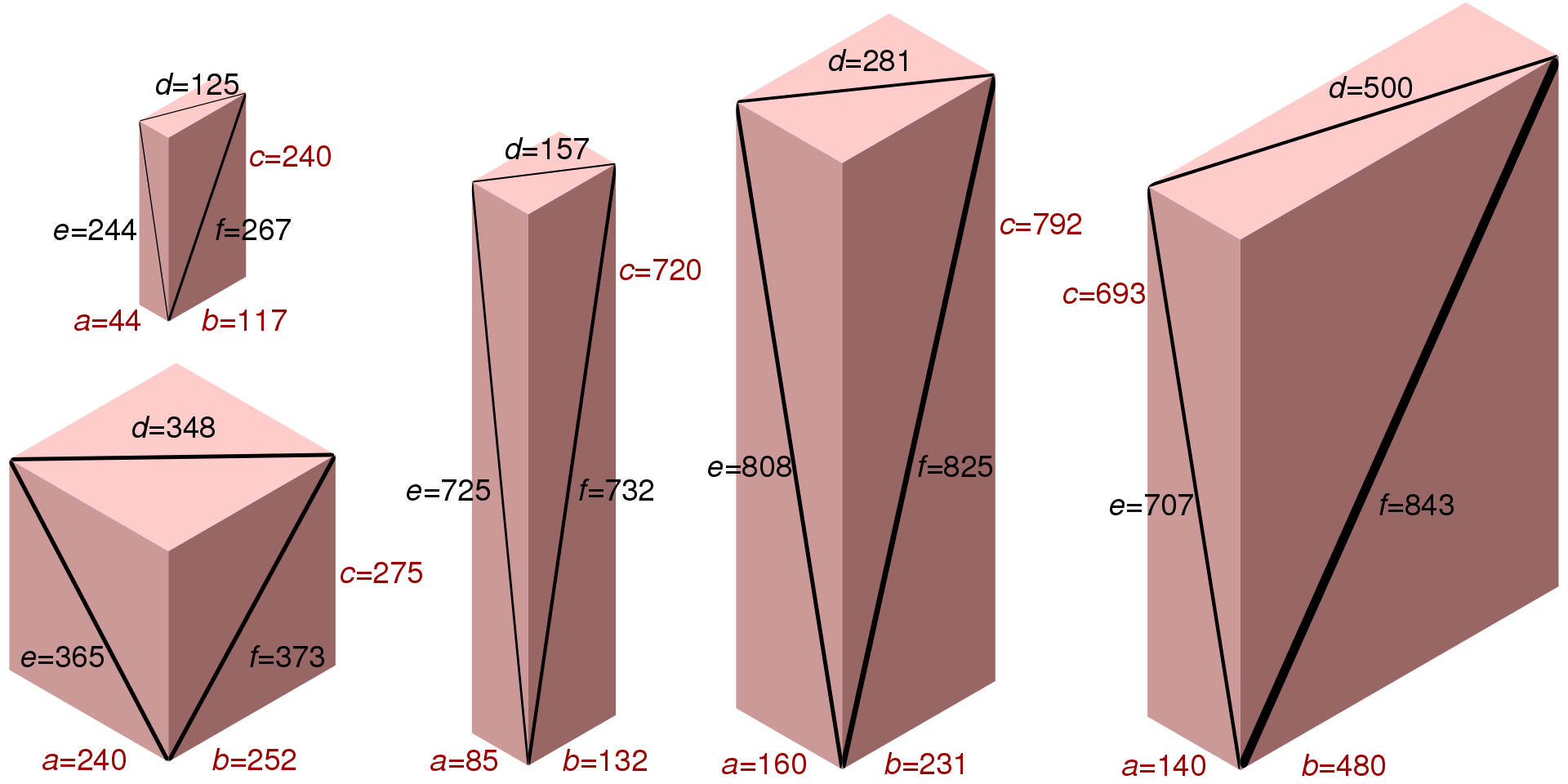
Если ответ "да", то тогда эти числа образуют рёбра совершенного кубоида, то есть прямоугольного параллелепипеда, у которого все рёбра, их диагонали, а также основная диагональ целые числа.
Прямоугольные параллелепипеды, рёбра и диагонали ребёр которых целые числа, называются параллелепипедами Эйлера. Например, таким параллелепипедом является параллелепипед с рёбрами 240, 117 и 44.
Действительно,
117^2 + 44^2 = 125^2;
240^2 + 44^2 = 244^2;
240^2 + 117^2 = 267^2
Однако чётвертое условие не выполняется: не является квадратом целого числа.
Если совершенный кубоид существует, он должен выполнять несколько условий:
Одно из чисел делится на 4, другое на 16;
Одно из чисел делится на 3, другое на 9;
Одно из чисел делится на 5;
Одно из чисел делится на 11;
Компьютерный перебор проверил все значения ребёр до , но пока никаких кубоидов не нашёл.
Однако, гипотезу это не опровергает.
Если для любого натурального числа n число составное, то k является числом Серпинского. Верно ли, что 78557 наименьшее число Серпинского?
Да, может показаться удивительным, но такие числа существуют. Например, доказано, что всегда будет делиться либо на 3, либо на 5, либо на 7, либо на 13, либо на 19, либо на 37, либо на 73.
На данный момент известно лишь 5 чисел, меньших 78557, и которые могут быть числами Серпинского. Это 21881, 22699, 24737, 55459 и 67607.
Кстати, именно с числами Серпинского связано нахождение одного из самых больших простых чисел - речь идёт про .
Подумайте, если бы наука ограничилась бы только перебором n до 31172164, то она бы заявила, что 10223 является числом Серпинского. И была бы неправа.
Я считаю, что эта гипотеза учит нас, что перебор надо доводить до конца, а поспешных заявлений делать не стоит.